Histogram to wektor wartości obrazujący liczność elementów występujących w danym przedziale wartości np. liczba mężczyzn o wzroście w przedziale \(<1,70-1,75)\). Najczęściej utożsamia się histogram z wykresem słupowym służącym do jego wizualizacji, ale sam histogram jest właśnie wektorem liczności nie wykresem.

Jak wyliczyć histogram?

W jaki sposób napisać funkcję, która wyliczy nam histogram z dowolną liczbą przedziałów. W naszym rozumieniu histogram jest wektorem zawierającym sumę pikseli, które należą do poszczególnych przedziałów jasności w obrazie. Jako wejście funkcja powinna otrzymać obraz oraz liczbę przedziałów, na jakie podzielimy obraz.

def fhistogram(img, N):
    ############
    return H

Wyliczony histogram warto wyświetlić w celu sprawdzenia jego poprawności. Najlepiej wykorzystać do tego funkcję: plt.bar()

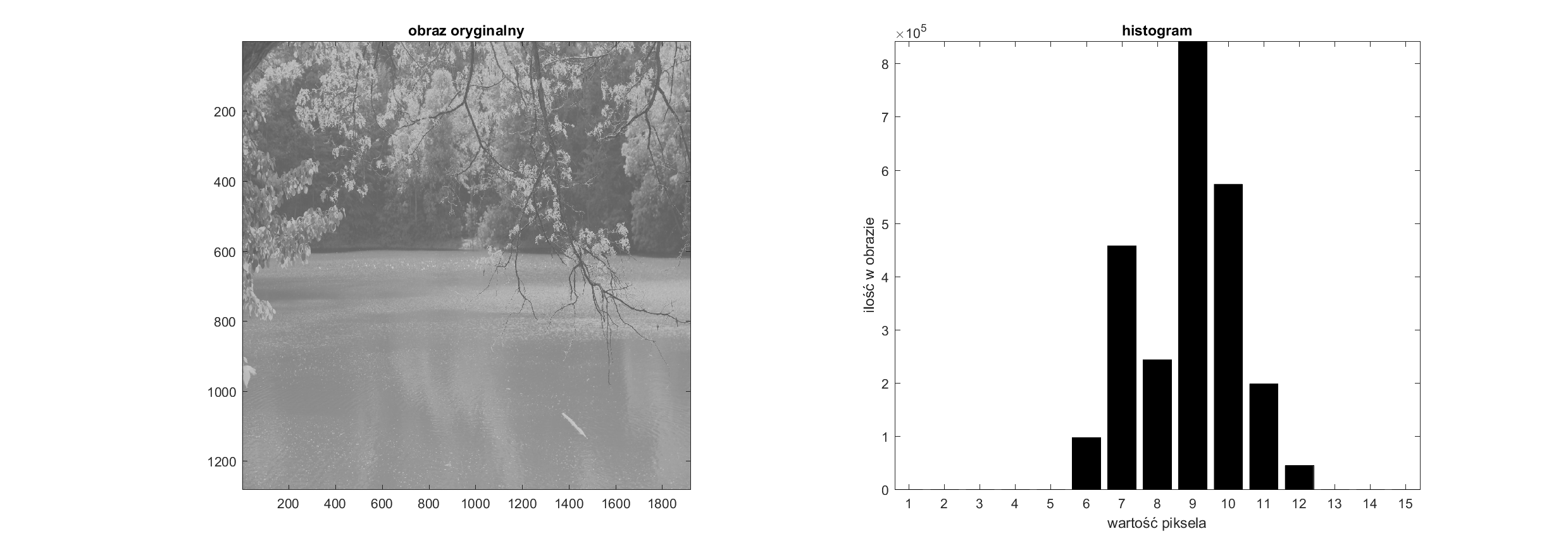
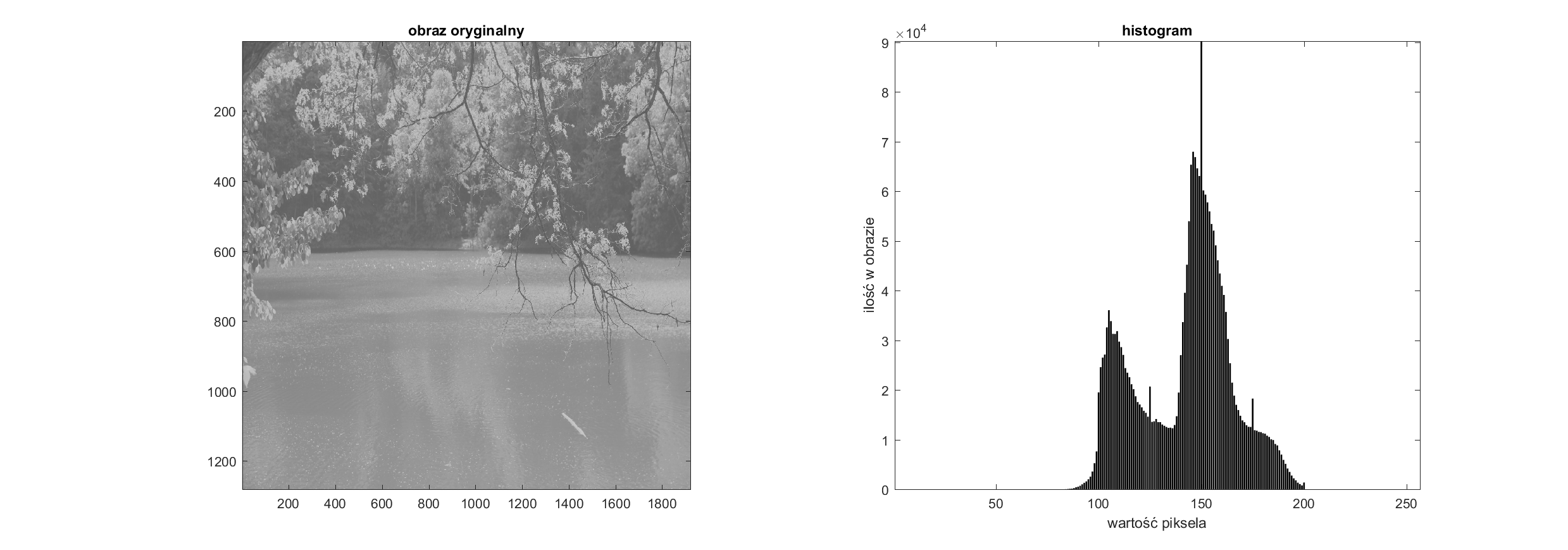
Do obliczeń tak wyliczony histogram jest oczywiście najdokładniejszy. Jednak przed wyświetleniem warto przeprowadzić normalizację, która ułatwia wzajemne porównywanie histogramów, na przykład w ten sposób:

Hp=H.copy()/np.sum(H);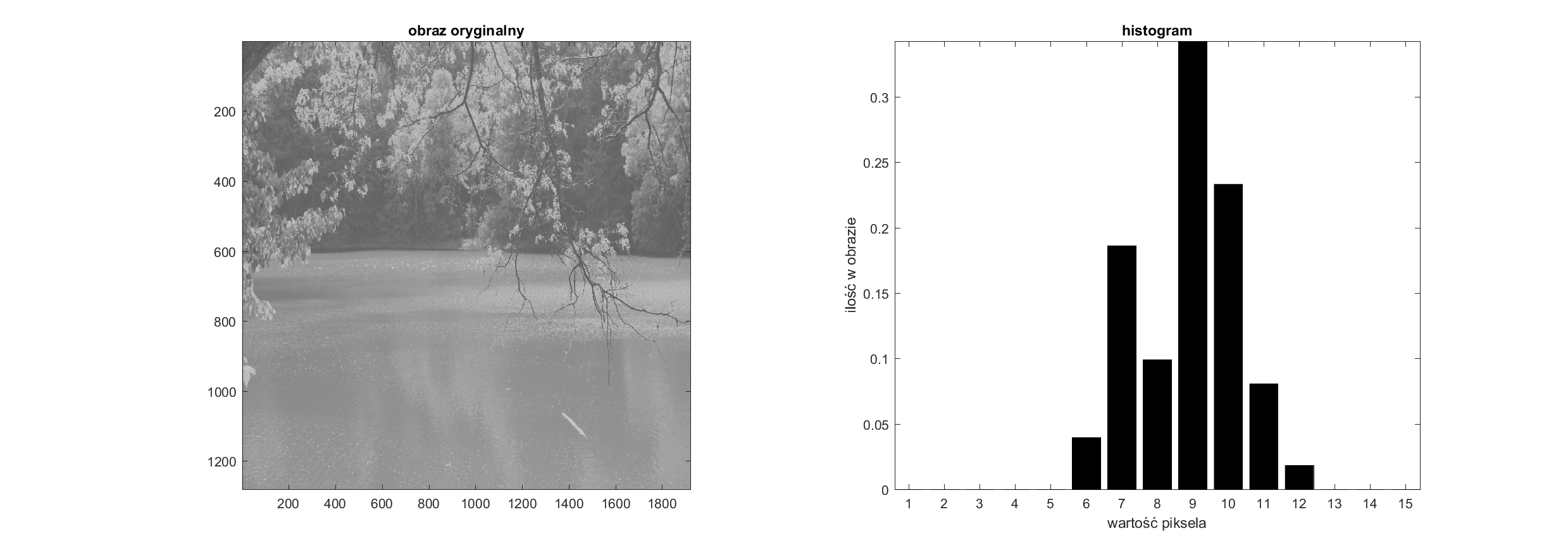

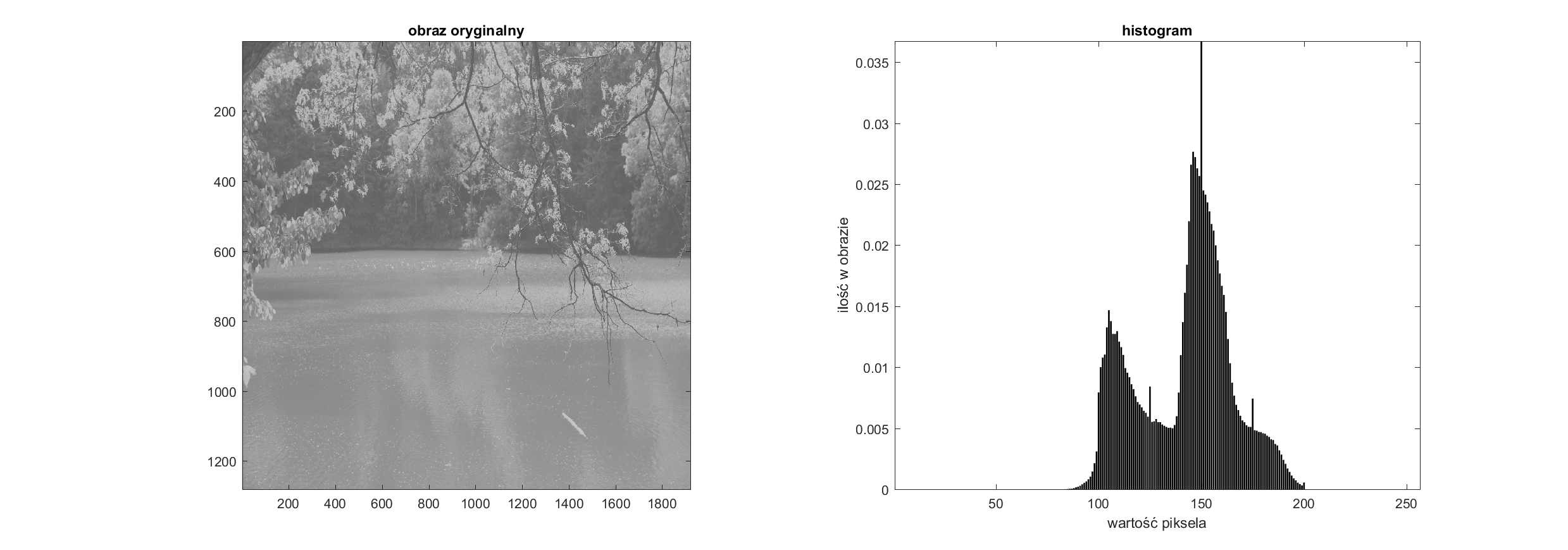
Podpowiedź 1

Podczas liczenia warto wykorzystać macierze logiczne. W jaki sposób można ich użyć? Polecam wkleić poniższy kod i zastanowić się nad jego działaniem:

a = np.random.rand(5, 5)
print(a > 0.33)
print(a < 0.55 )
print((a > 0.33) & (a < 0.55))

Tylko jak to wszystko zliczyć?

Podpowiedź 2

W przypadku problemów z wyliczeniem odpowiednich przedziałów dla histogramu można wykorzystać funkcję: np.linspace(a, b, c)

W jaki sposób? Polecam przeczytać informacje z pomocy dotyczącej tej funkcji oraz zastanowić się nad sposobem podziału odcinka poniżej. Dokładniej w zależności od ilości przedziałów (odcinków) ile jest granic (pionowych kresek) w przypadku każdego podziału?

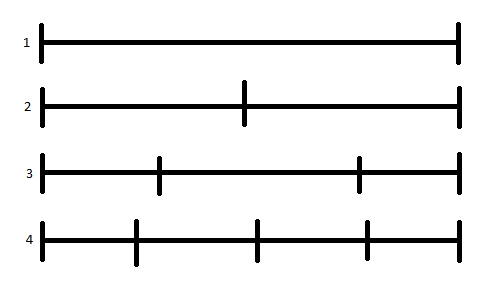
Czyli jeżeli mamy 3 przedziały to mamy 4 granice. Jeżeli mamy \(N\) przedziałów to nasze \(c\), czyli ilość granic będzie równa?

g=np.linspace(0, 1 or 255,c ) # ta linijka nie działa to jest przykład. 1 jest dla obrazów na float, 255 dla obrazów na uint8

Podpowiedź 3

Na pewno przyda się jedna pętla for, poniżej jej przykładowa składnia do połączenia z dwiema poprzednimi podpowiedziami:

for ii in range(0,N):
    print(g[ii],g[ii+1])

Test 1

Na prośbę studentów zamieszczam warunki testowe do sprawdzenia poprawności działania funkcji przy założeniu, że analizujemy obrazy w zakresie \(<0,255>\):

A = np.array([[1, 0, 0.25], [1, 0.75, 0.5], [1, 0.5, 0.25]]) * 255.0
print( A)
print( fhistogram( A, 3 )) # [3 2 4]
print( fhistogram( A, 5 ) )# [1 2 2 1 3]

Operacje na histogramie

Operacjami na histogramie nazywamy zbiór operacji na obrazie, które wykorzystują jako dane wejściowe histogram, a efekt ich działania można zaobserwować na histogramie obrazu po operacji. W celu uproszczenia obliczeń zakładamy, że operacje na histogramie będziemy wykonywać dla obrazów na uint8.

Rozciągnięcie — Liniowe i nieliniowe

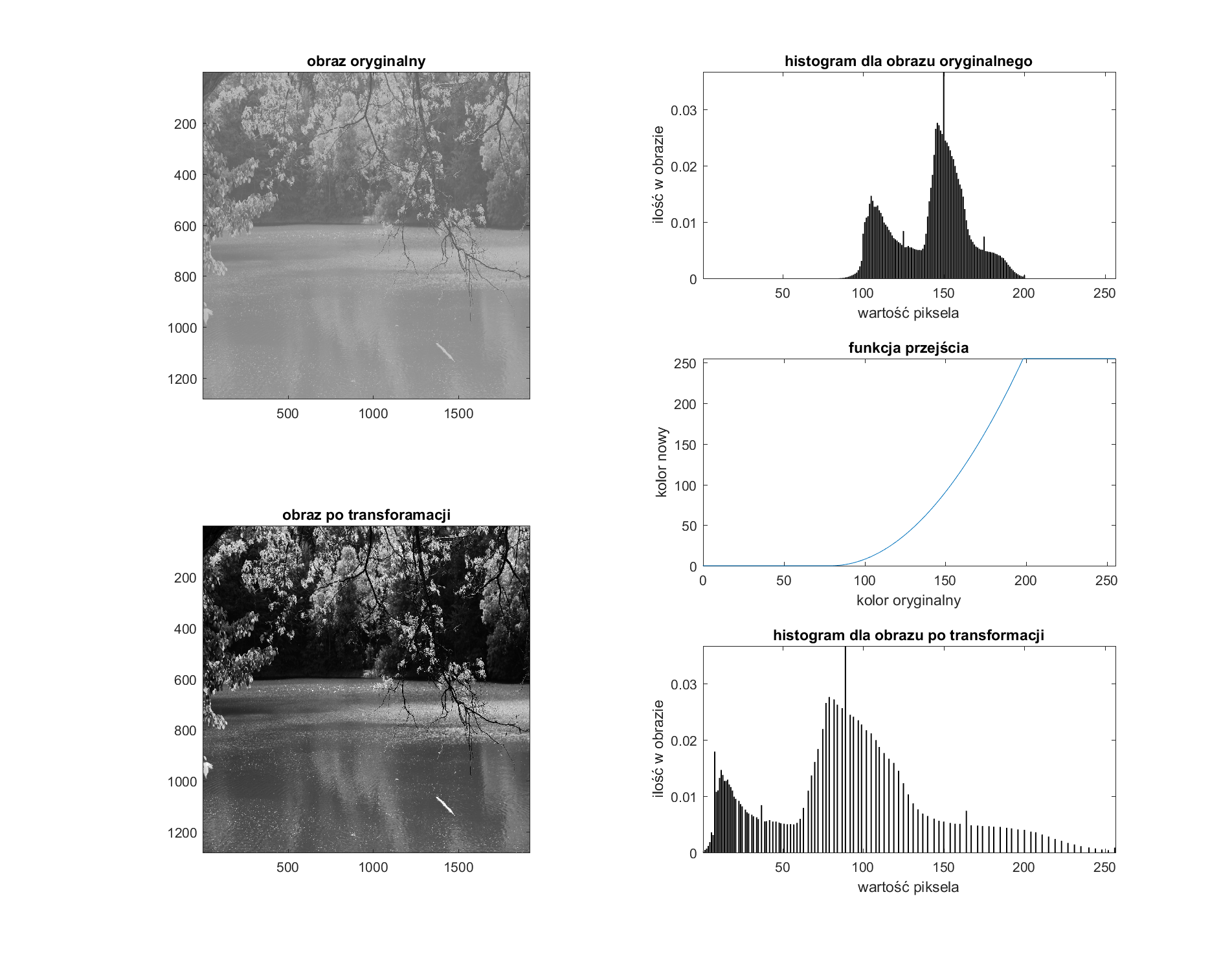
Pierwszą operacją to rozciągnięcie liniowe. To operacja mająca za zadanie przeliczyć wartości pikseli oryginalnego obrazu w taki sposób, aby w nowym obrazie zajmowały one znacznie szerszy zakres wartości. W przypadku rozciągnięcia liniowego wykorzystujemy w tym celu funkcję linową \(y=ax\). Należy pamiętać, że każda z operacji rozciągnięcia ma jakiś początek (\(x_1\)) i koniec (\(x_2\)) i właśnie dla takiego zakresu przeprowadzamy operacje. Można zatem pominąć parametr \(a\) we wzorze i modulować nachylenie prostej poprzez odpowiednie dobieranie parametrów \(x_1\) i \(x_2\). Poniżej zaprezentowano przykład rozciągnięcia liniowego:

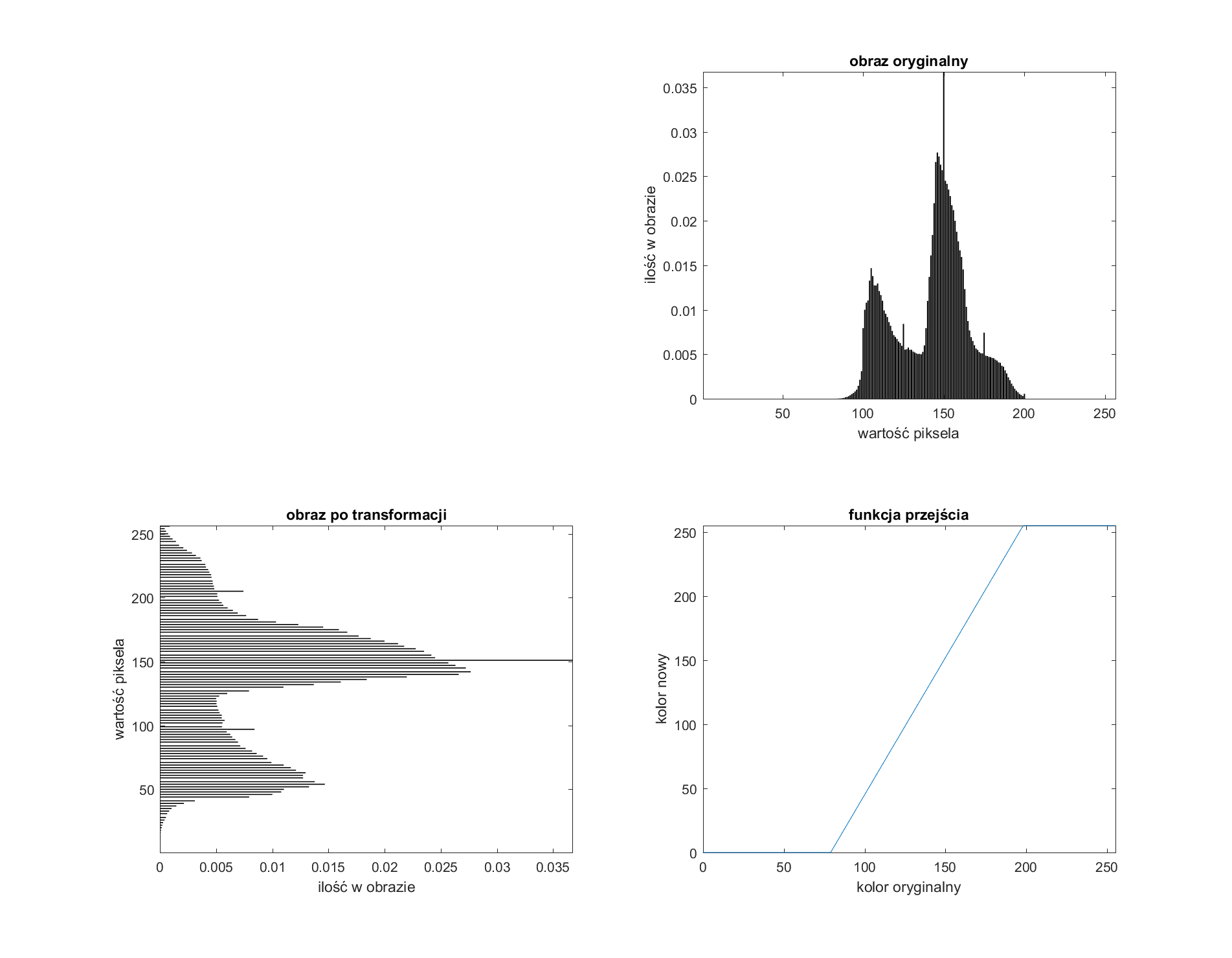
W prawym górnym rogu zaprezentowano histogram obrazu oryginalnego obrazu poniżej niego mamy zamieszczoną funkcję przejścia, czyli sposób, jaki mamy zmodyfikować wartości pikseli obrazu. W lewym dolnym rogu widać natomiast histogram obrazu już po modyfikacjach. Obserwując wykresy, można zauważyć i oszacować punkty \(x_1\) i \(x_2\). Na funkcji przejścia widać, że wszystkie wartości pikseli w obrazie poniżej \(x_1\) są zerowane, a powyżej \(x_2\) osiągają maksymalną wartość 255.  Poniżej zaprezentowano, jak wygląda to na obrazie rzeczywistym:

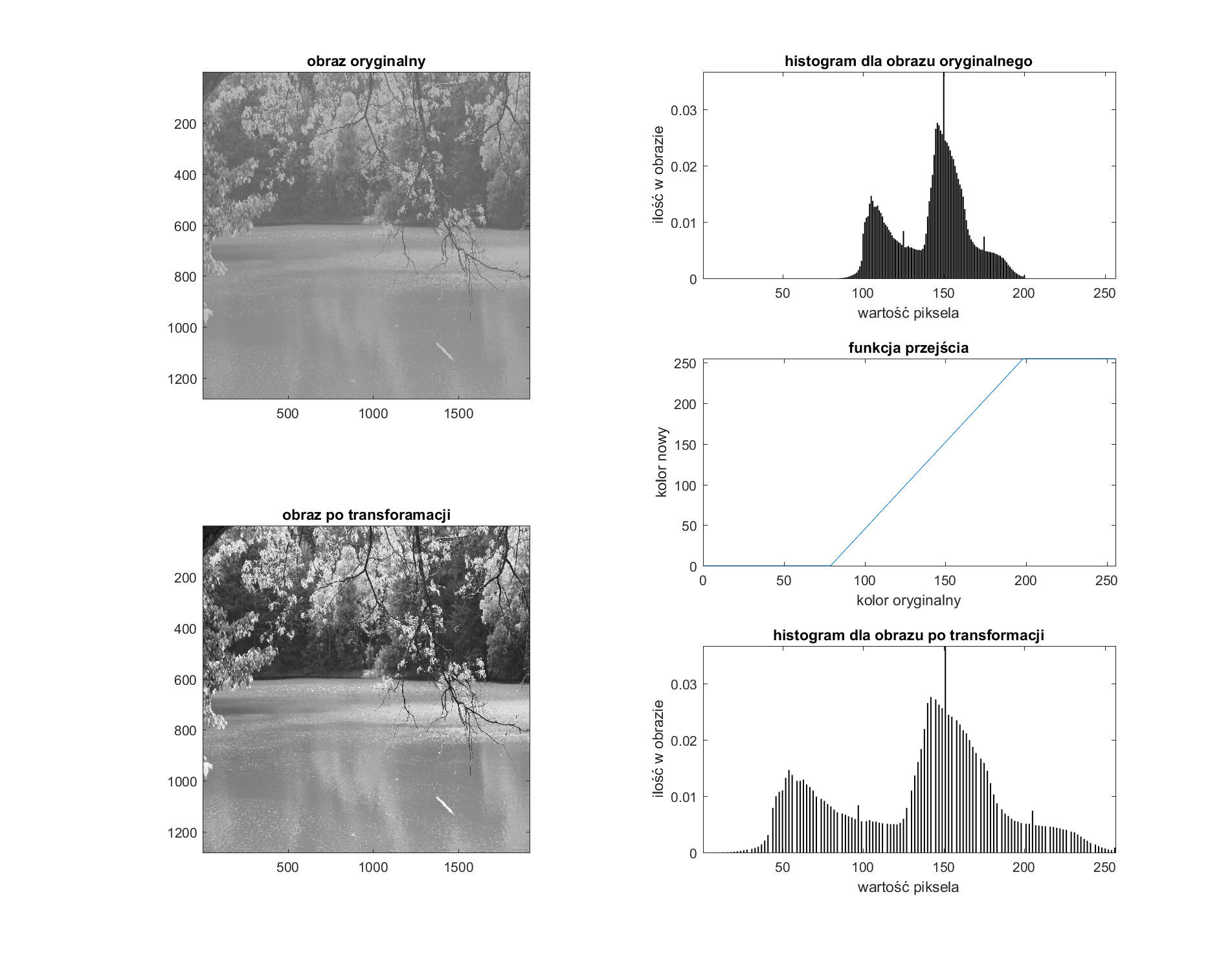
Wariacją na temat przekształcenia liniowego jest przekształcenie nielinowe. Zamieniamy tu funkcję liniową, zastępując ją funkcjami nieliniowymi np. \(y=x^{2}\), \(y=\sqrt{x}\), \(y=log(x)\), \(y=a^{x}\). Możemy modyfikować ich parametry, zmieniając “ostrość” krzywej. Należy jednak pamiętać, że w dalszym ciągu mamy jakiś punkt początkowy i końcowy \(x_1\) i \(x_2\). W ogólnym przypadku krzywe prezentują się w poniższy sposób:

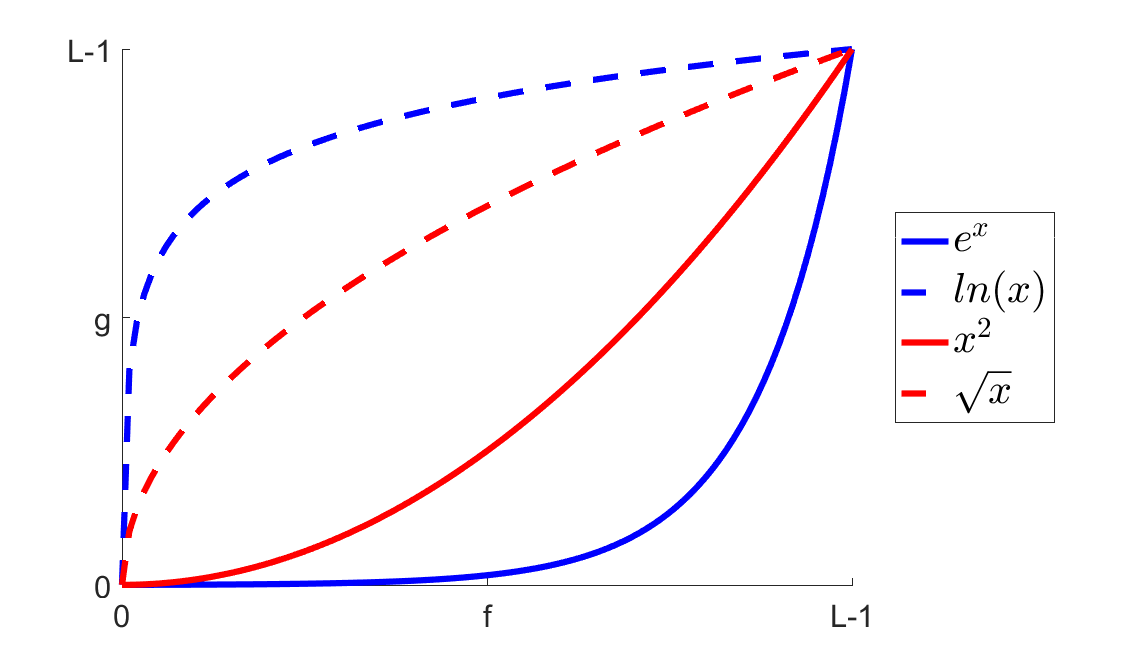
Poniżej pokazano przykład działania pewnej funkcji, aby pokazać, jak to powinno wyglądać:

Generowanie wzorca i jego stosowanie

Wzorzec naszego przekształcenia składa się z 3 części:

1. Dla wszystkich wartości poniżej \(x_1\) ustawiamy minimum - 0.
2. Dla wszystkich wartości powyżej \(x_2\) ustawiamy maksimum - 255.
3. Dla pozostałych wartości generujemy nasze przekształcenie.

Poniżej dwa przykłady generowania takiej mapy przekształceń liniowa oraz nieliniowa (sugeruję wykorzystać te wzory i przerobić je sobie na funkcję):

x1=23
x2=130

W_lin=np.zeros((256,))
W_exp=np.zeros((256,))

W_lin[x2:]=255
W_exp[x2:]=255

W_lin[x1:x2]=np.linspace(0,1,x2-x1)*255
e=np.exp(3*np.linspace(0,1,x2-x1)) # e^(3x)
e-=np.min(e)
e/=np.max(e)
W_exp[x1:x2]=e*255

W_lin=W_lin.astype(np.uint8)
W_exp=W_exp.astype(np.uint8)

plt.plot(np.linspace(0,255,256),W_lin)
plt.plot(np.linspace(0,255,256),W_exp)

plt.show()

W jaki sposób nałożyć nasz wzorzec na nowy obraz? Poniższy kod działa dla 1-warstwy!

img_out=img.copy()
for c in range(256):
    img_out[img==c]=W[c]

Wyrównie Histogramu

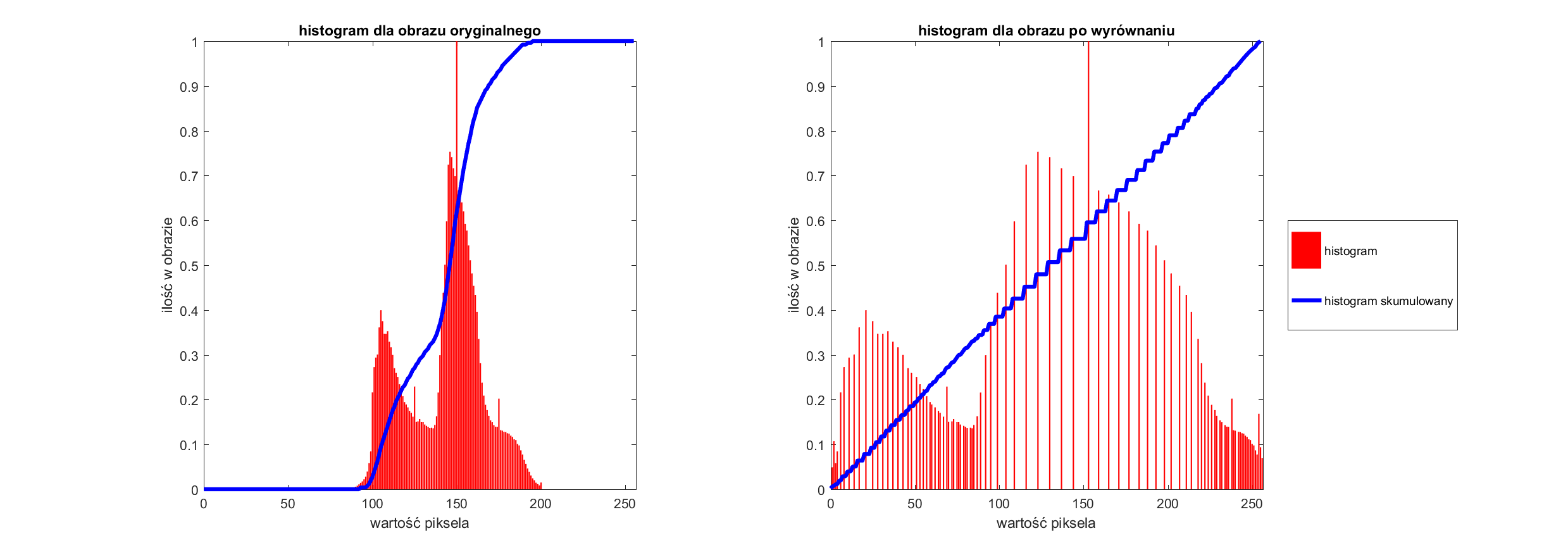
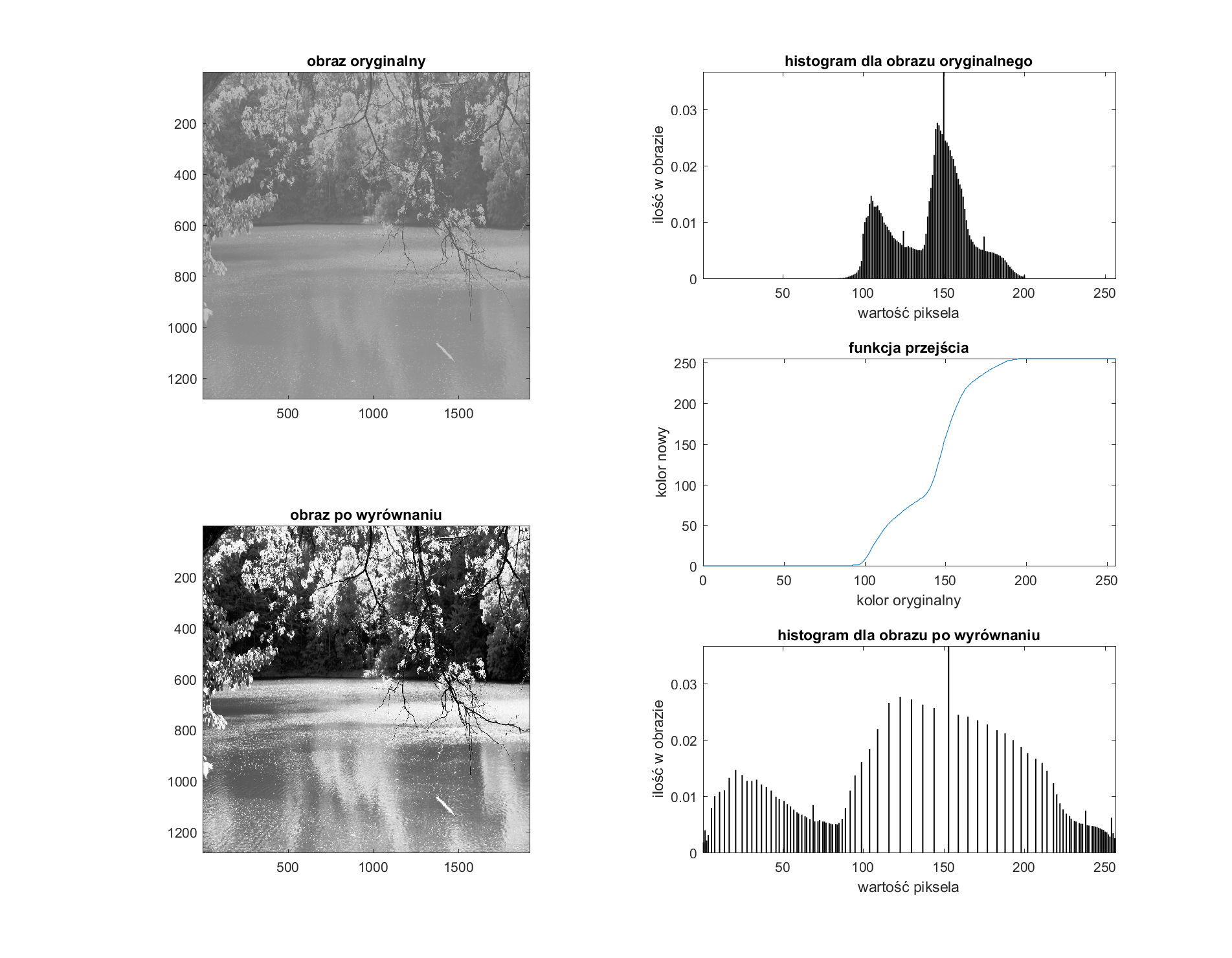
Wyrównanie histogramu to jedna z operacji na histogramie, która ma za zadanie poprawić kontrast obrazu. Metoda wykorzystuje tzw. histogram skumulowany (dystrybuantę) i na jego podstawie pozwala wyliczyć nowe wartości dla pikseli.

Działanie pisanej funkcji zaczynamy od wyliczenia histogramu skumulowanego (dystrybuanty). Wyliczamy ją według wzoru: \(d(i)=\sum_{j=1}^{i}h(j)\) , gdzie \(h\) jest histogramem obrazu źródłowego (bez normalizacji). Można w tym celu wykorzystać funckję np.cumsum

Przed zabraniem się do wyliczania nowych wartości pikseli potrzebujemy znać jeszcze jedną wartość \(dfmin\), czyli pierwszą wartość dystrybuanty różną od 0. Można do tego wykorzystać funkcję:

be = np.where(d > 0)
print (be)
print (be[0][0]) # first
print (be[0][-1])# last

Co oznaczają współczynniki tej funkcji? Co ona zwraca?

Nowe wartości pikseli wyliczamy za pomocą wzoru \(hv(i)=round(\frac{d(i)-dfmin}{(M*N)-dfmin}*(L-1))\) gdzie \(M,N\) to rozmiar analizowanego obrazu, a \(L\) to dostępna ilość kolorów (w naszym przypadku 256). Algorytm został dokładniej rozpisany na wikipedii. Poniżej zaprezentowano graficzne przejście pomiędzy obrazami. Na czerwono narysowane są histogramy na czarno histogram skumulowany. Dodatkowo na ostatnim rysunku zaprezentowano wynik działania algorytmu. Nasze \(hv\) nakładamy na obraz tak samo, jak nasze rozciągnięcia histogramu.

Praca z obrazem kolorowym

Operacje są raczej przystosowane do pracy z obrazami w skali odcieni szarości, ale nic nie stoi na przeszkodzie do zastosowania ich na obrazach kolorowych. Można poddać działaniu wszystkie warstwy albo niektóre z nich. Przykładowo dobre efekty można osiągnąć działając na warstwie Y w obrazie YCbCb albo na warstwie L obrazu w CIE Lab oraz na warstwie V obrazu w HSV.