W podejściu praktycznym filtracja splotowa obrazu wymaga od nas dwóch elementów wejściowych. Jednym jest obraz filtrowany, drugim maska filtru, z jakim chcemy dokonać splotu. Czyli nasza funkcja powinna mieć wejście podobne do poniższego:

def ffitlter(img, mask):

W ramach operacji splotu mnożymy otoczenie piksela, dla którego chcemy otrzymać wartość przez maskę i sumujemy wartości.

Załóżmy, że mamy maskę \[\begin{bmatrix} 1 & 1 & 1 \\1 & 4 & 1 \\ 1 & 1 & 1 \end{bmatrix}\] i załóżmy, że sąsiedztwo piksela (czerwony), dla którego chcemy, obliczyć wartość splotu prezentuje się następująco:

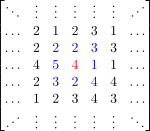
Ponieważ rozmiar naszej maski wynosi 3x3 to takie samo otoczenie naszego piksela będzie musiało brać udział w wyliczaniu wartości splotu. Obszar ten został zaznaczony na niebiesko.

Nasz splot obliczmy za pomocą wzoru \(s[i,j]=\dfrac{\sum_{a}\sum_{b}p[i+a,j+b]*M[a,b]}{N}\), gdzie:

• \(s\) to obraz po filtracji,
• \(p\) obraz przed filtracją,
• \(M\) maska,
• \(N\) norma maski.

Norma maski przyjmuje wartość równą sumie wartości elementów maski lub 1 w przypadku, gdy suma ta wynosi 0, co zostało opisane wzorem: \[ N= \begin{cases} 1 & \text{,gdy} \sum M = 0 \\ \sum M & \text{,w pozostałych przypadkach}\\ \end{cases} \]

W naszym przypadku gotowe równanie będzie wyglądało tak:

\[s'=\dfrac{2*1+2*1+3*1+5*1+4*4+1*1+3*1+2*1+4*1}{12}=\dfrac{38}{12}=3\dfrac{1}{6}\approx3.1667\]

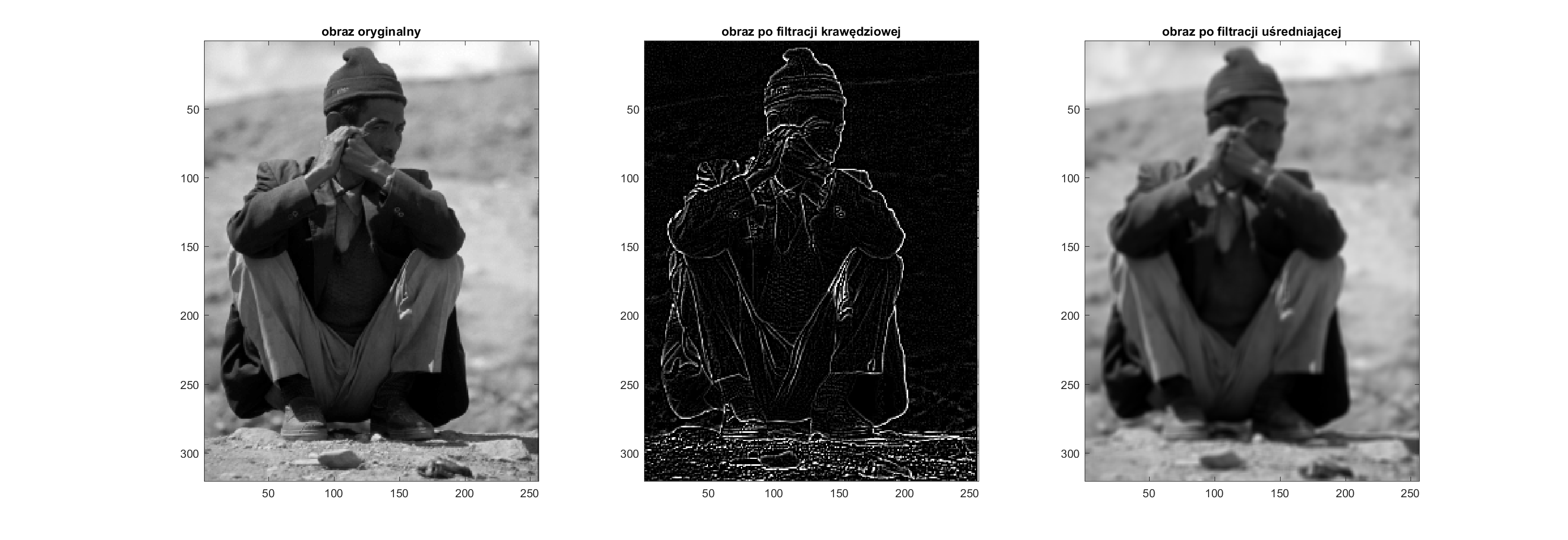
Najczęściej filtry, których suma jest większa niż 0 to filtry rozmywające, a te sumujące się do 0 to filtry krawędziowe. Przykład działania obu filtrów zaprezentowano poniżej.

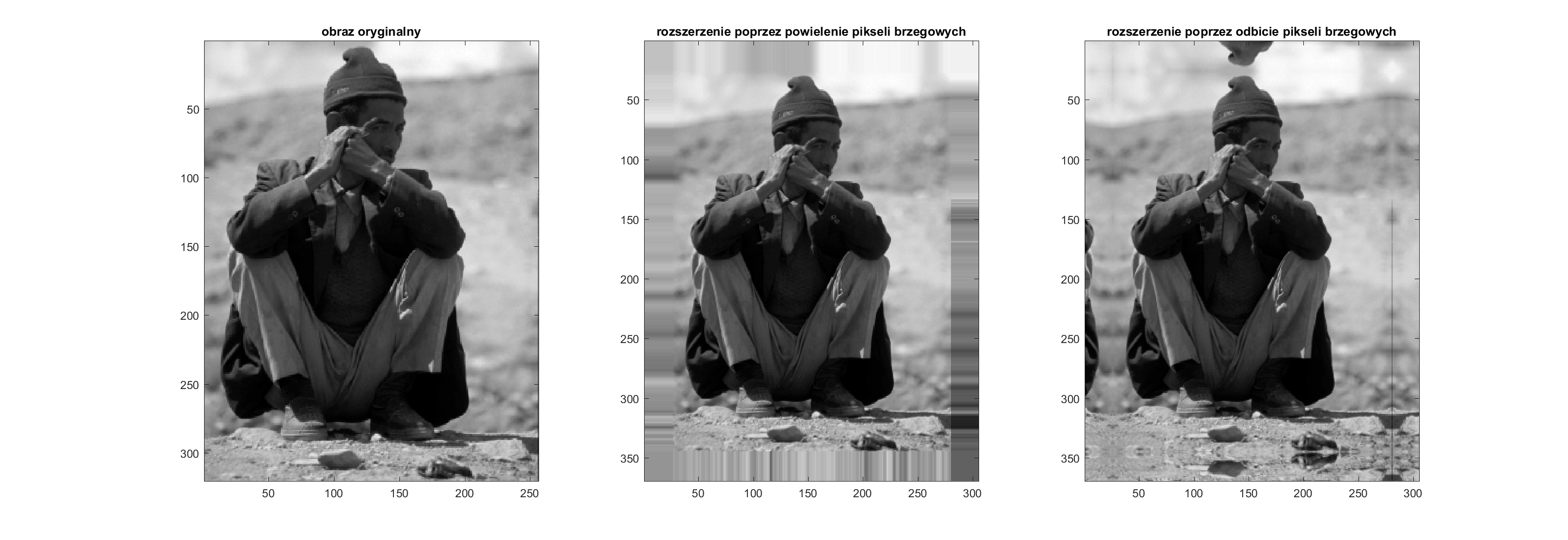
Problem pojawia się przy brzegach obrazu, ponieważ nie ma możliwości nałożenia maski na piksele bliżej krawędzi obrazu, dlatego należy wprowadzić jedną z dwóch metod powielania pikseli brzegowych zaprezentowanych na poniższym obrazie. Do wyboru są dwie metody powielenie pikseli brzegowych lub odbicie pikseli brzegowych (zalecane).

Od czego zależny jest rozmiar powiększanego obrazu?

Wszystko zależy od maski, a dokładniej od tego, który jej element przyjmujemy jako jej środek. Najłatwiej wyobrazić sobie, maskę nałożoną w lewym górnym oraz prawym dolnym rogu obrazu. Można w ten sposób zobaczyć zasadę, która pokazuje o jaki rozmiar należy powiększyć obraz. W ramach ćwiczenia można zastanowić się nad rozmiarami powiększenia obrazu dla poniższych masek . W ramach podpowiedzi możliwe “środki” masek zaznaczono w (). Dla ułatwienia znalezienia reguł maski są niesymetryczne.

\[\begin{bmatrix} 1 & 1  \\(1) & (1)  \\ 1 & 1  \end{bmatrix}\]

\[\begin{bmatrix} 1 & 1 & 1 & 1  \\1 & 1 & 1 & 1  \\ 1 & (1) & (1) & 1  \\ 1 & 1 & 1 & 1  \\ 1 & 1 & 1 & 1   \end{bmatrix}\]

\[\begin{bmatrix} 1 & 1 & 1 & 1 & 1 \\1 & 1 & 1 & 1 & 1  \\ 1 & 1 & (1) & 1 & 1 \\ 1 & 1 & (1) & 1 & 1 \\ 1 & 1 & 1 & 1& 1 \\ 1 & 1 & 1 & 1 & 1  \end{bmatrix}\]

Porada 1

W jaki sposób oszacować nasze odległości w każdym kierunku? Zaczynamy od wyznaczenia sobie środka, który znajduje się mniej więcej w środku. Rozpatrzmy sobie dwa jednowymiarowe przypadki a - 1x5 oraz b - 1x6. Jeżeli wymiar równy jest \(1\) nie potrzebujemy znajdować środka, ponieważ jest on naszym jednym pikselem w tym wymiarze. W każdym innym przypadku musimy wyliczyć środek. Robimy to poprzez podzielenie naszego wymiaru przez 2 i zaokrąglenie go do jakiegoś adresu całkowitego: np.round, np.floor (sugeruję ten) lub np.ceil. W przypadku A będą to po kolei zaokrąglenia \(x=2,(2),3\), dla przypadku B będą to zaokrąglenia \(x=3,(3),3\). Jak mamy już współrzędną naszego środka, to na tej podstawie możemy wyliczyć odległości, o ile musimy poszerzyć nasz obraz. Jeżeli mamy wymiar równy \(1\) to nie musimy nic powiększać, w każdym innym przypadku potrzebujemy dwie wartości, określające o ile musimy powiększyć nasz obraz w obu kierunkach dla naszego wymiaru. Podstawową zasadą jest spełnianie się równania: \(w=x1+x2+1\). Czyli dla przypadku gdzie maska ma rozmiar \(1\) nasze równanie, będzie wyglądać tak: \(1=x_1+x_2+1 \rightarrow 1-1=x_1+x_2 \rightarrow 0=x_1+x_2\), czyli \(x_1=x_2=0\).

Skąd wziąć wartość \(x1\)? Najłatwiej wziąć współrzędną środka i ponieważ indeksujemy od \(0\) to współrzędna, będzie jednocześnie ilością elementów przed tą współrzędną. A jeżeli mamy już nasze \(x_1\), to na jego podstawie możemy wyliczyć \(x_2\), przekształcając powyższy wzór \(x_2=w-x1-1\).

Porada 2

Znając rozmiar rozmiary, o jakie należy powiększyć posiadany obraz można zbudować nowy obraz poprzez np. budując nową macierz obrazu w taki sposób \(\begin{bmatrix} A & B & C \\D & org & E \\ F & G & H \end{bmatrix}\), gdzie macierze od A do H są macierzami, o które należy poszerzyć obraz oryginalny i wypełnionymi właściwymi danymi. Natomiast \(org\) to oryginalny obraz. Konkatenację wykonujemy w następujący sposób:

A=np.ones((2,3))
B=np.ones((3,3))+1
C=np.ones((2,2))+2
D=np.ones((3,2))+3

AB=np.concatenate((A,B), axis=0)
CD=np.concatenate((C,D), axis=0)
AC=np.concatenate((A,C), axis=1)
BD=np.concatenate((B,D), axis=1)

print AB
print CD
print AC
print BD

Dodatkowo przypomnienie sposobu adresowania w Pythonie, jaki może się przydać podczas wykonywania zadania:

A=np.array(range(0,10))
print (A)
print (A[(3):0:-1] )
print (A[-2:-(3+2):-1])
# składnia [początek:koniec:krok] - z drobnymi modyfikacjami co do wartości warto potestować

Porada 3

Sama operacja splotu obrazu z maski nie wymaga do działania więcej niż dwóch pętli! Można wykorzystać funkcję np.multiply i funkcję np.sum

Pętle polecam robić po wymiarach niepowiększonego/wyjściowego obrazu. Ponieważ jeżeli uwzględnimy wszystkie przesunięcia wynikające z przesunięcia obrazu i rozmiaru maski osiągniemy te same współrzędne, jak je pomijając i wyliczając otoczenie w poniższy sposób:

ex_img[w+0:M_w,k+0:M_k]