Filtracja w dziedzinie częstotliwości to zbór operacji na widmie Fouriera obrazu polegających na modyfikacji lub zerowania niektórych (pasm) częstotliwości w celu uzyskania odpowiednich efektów po powrocie do przestrzeni obrazu.

Podstawowe operacje

Pracę z obrazem w dziedzinie częstotliwości zaczynamy od poznania kilku funkcji, które są nam potrzebne do pracy:

np.fft.fft2(img)
np.fft.ifft2(widmo)
np.real(widmo)
np.abs(widmo)
np.fft.fftshift(widmo)
np.fft.ifftshift(widmo)

• fft2 to dwuwymiarowa szybka transformata furiera, która służy do przejścia z dziedziny rzeczywistej do dziedziny częstotliwości;
• ifft2 to funkcja odwrotna do fft2, czyli przejście z dziedziny częstotliwości do dziedziny rzeczywistej;
• funkcje real i absolute mogą być przydatne podczas wyświetlania obrazu przetworzonego oraz widma;
• o funkcjach fftshift i ifftshift powiemy za chwilę.

Teraz w ramach zadania należy wykonać kilka kroków, które będą powtarzane wielokrotnie w kolejnych etapach:

1. Wczytanie i przygotowanie obrazu — wyświetlić obraz
2. Wyliczenie widma — również wyświetlić. Do wyświetlania jest potrzebna funkcja np.abs, bo niemożemy wyświetlać wartości zespolonych naktórych wykonujemy obliczenia.
3. !!! w tym miejscu będą dokonywane wszystkie modyfikacje widma, które w tym momencie pomijamy
4. Przeprowadzamy operację powrotną z dziedziny częstotliwości — efekt również wyświetlamy, po niektórych operacjach może być wymagane użycia funkcji np.real. Można tę operację wykonywać zawsze, nie popsuje ona wyników.

Do obliczeń warto wykorzystywać zmienne w zakresie wartości naszego obrazu z przedziału \(<0,1>\) dla funkcji fft2. Należy dokonać tego poprzez podzielenie wartości pikseli w całym obrazie przez \(255\) dla obrazów na uint8.

Jak wyświetlać widmo

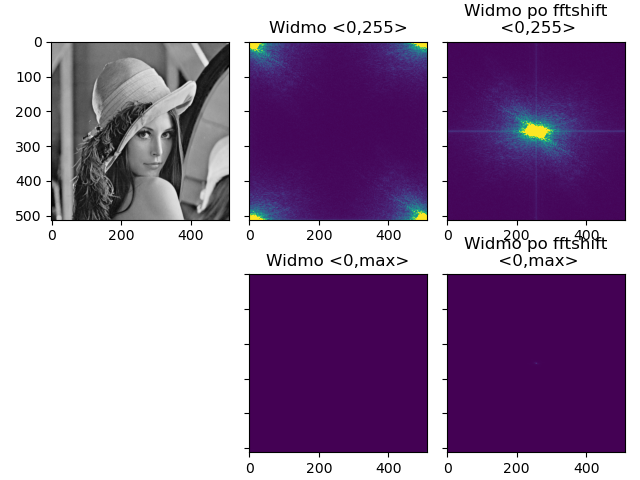
Pomówmy chwilę o widmie obrazu aktualnie jego środek znajduje się w punkcie \((0,0)\) macierzy. W celu ułatwieniu odbioru obrazu widma wykorzystujemy funkcje fftshift oraz ifftshift. Pierwsza służy do przesunięcia środka widna do centrum macierzy. Druga natomiast realizuje operację odwrotną.

Z wyświetlaniem może być kilka problemów — pierwszy widmo jest zapisane na flotat i liczbach zespolonych, więc już na starcie jest problem z wyświetleniem (liczby zespolone i clipping do \(1\)), dlatego trzeba zastosować wartości bezwzględne oraz podawać jakieś parametry vmax=?. Warto sprawdzić różnego rodzaju wartości (\(255\), maksymalna wartość widma etc.).

• Co widać na takim widmie do w przestrzeni <0,max>?
• O czym może to świadczyć?

W jaki sposób przeprowadzać filtrację?

Wszystkie filtracje widma przeprowadzamy na 3 etapie naszego algorytmu. Pamiętać, żeby dane dalej były na liczbach zespolonych (wartości bezwzględne są potrzebne tylko do wyświetlania). Filtracje przeprowadzamy je poprzez stworzenie maski filtra o rozmiarze naszego widma. Maska zawiera \(0\) i \(1\) w odpowiednich miejscach zgodnie ze schematami przedstawionymi poniżej. Najłatwiej można to dokonać przy wykorzystaniu mnożenia elementu przez element.

np.multiply(matrix1, matrix2)

Wszystkie schematy zakładają, że centrum widma znajduje się w centrum macierzy, dlatego wymagane będzie użycie funkcji przesuwających centrum widma. Schematy mają wartości oryginalnego widma (niebieskie) oraz elementy wyzerowane (białe). Można je wykorzystać jako maskę do wymnażania z wartościami \(1\) w miejscach żółtych oraz wartościami \(0\) w miejscach białych. Są one symetryczne względem obu osi — to znaczy, że można wygenerować tylko jedną ćwiartkę i ją odpowiednio powielić. Celem zadania jest takie dobranie parametrów (rozmiarów pól niebieskich i białych), żeby osiągnąć jak najlepsze efekty. Można je osiągnąć na więcej niż jednej masce.

Poniżej przykład funkcji generowania masek:

def buildM2(shape,w1,w2,k1,k2,flip=False):
    Q=np.zeros((shape[0]//2,shape[1]//2))
    Q[0:(w2+1),k1:(k2+1)]=1
    Q[w1:(w2+1),0:(k2+1)]=1
    QQ=np.concatenate((Q,Q[:,::-1]),axis=1)
    O=np.concatenate((QQ,QQ[::-1,:]),axis=0)
    if flip:
        O=np.logical_not(O)*1
    return O

def buildM3(shape,R,flip=False):
    Q=np.zeros((shape[0]//2,shape[1]//2))
    angle=np.arange(0,np.pi/2,0.05)
    X=np.round(R*np.sin(angle)).astype(int)
    Y=np.round(R*np.cos(angle)).astype(int)
    for i in range(len(X)):
        Q[X[i],Y[i]]=1
    for row in range(Q.shape[0]):
        qrow= np.where(Q[row,:]>0)[0]
        if np.any(qrow):
            Q[row,:qrow[-1]]=1
    Q=Q[::-1,::-1]
    QQ=np.concatenate((Q,Q[:,::-1]),axis=1)
    O=np.concatenate((QQ,QQ[::-1,:]),axis=0)
    if flip:
        O=np.logical_not(O)*1
    return O