Uwaga Wykonanie tego zadania wymaga dobrze zrobionego filtracji splotowej.

Obróbka wstępna

Przed wykonaniem transformacji Hough`a należy wykonać dwa kroki przygotowawcze:

• Konwersja obrazu do skali odcieni szarości
• Wykrywanie krawędzi (filtracja splotowa)

Oba te etapy powinny skutkować dobrym wykryciem wszystkich krawędzi (zwłaszcza okręgów). Warto na tym etapie wyświetlać obraz w celu weryfikacji. Najlepiej wykorzystać filtr krawędziowy składający się z kilku masek, który został wybrany jako najlepszy w poprzednim zadaniu.

Przydatną operacją podczas tego etapu może okazać się operacja progowania:

poProgowaniu = (przedProgowaniem >= próg).astype('float64')

Może to pomoc oczyścić obraz z niechcianych krawędzi oraz wzmocni krawędzie, które są słabo widoczne. Poza tym na kolejnym etapie najlepiej posiadać macierz binarną obrazu zawierającą \(1\) w miejscach, gdzie istnieje krawędź.

Transformacja Hough`a

Zanim przejdziemy do samego algorytmu kilka słów na temat samej funkcji. Funkcja przyjmuje za parametr obraz kolorowy, zakres promieni, jaki ma zostać przeszukany oraz liczbę okręgów, jaką ma zwrócić. Jako wyjście program powinien zwrócić listę znalezionych okręgów (może być w postaci macierzy). Lista powinna zawierać promienie znalezionych okręgów oraz współrzędne ich środków. Lista powinna być już wstępnie przefiltrowana w celu usunięcia “fałszywych” detekcji, ale to zagadnienie zostanie jeszcze poruszone później. Jeżeli znalezionych okręgów będzie mniej niż liczba poszukiwanych okręgów, należy zwrócić tylko te znalezione w przeciwnym przypadku tylko te, które są najbardziej prawdopodobne. Funkcja powinna zatem wyglądać mniej więcej tak:

def ht(img, rmin, rmax, N):

Zakres przeszukiwanych promieni to \(<rmin,rmax>\), z dowolnym krokiem. Należy pamiętać, żeby przed wywołaniem pętli po tym zakresie wykonać obróbkę wstępną obrazu. Zakładamy na tym etapie, że posiadamy obraz krawędziowy zawierający \(0\) we wszystkich miejscach, w których nie ma krawędzi, a wartość \(1\) lub \(255\) (w zależności od przyjętej metodologii pracy).

Algorytm

Sama transformacja Hough`a działa dla konkretnego promienia, który będziemy nazywać dalej \(ir\). Metoda zakłada zbudowanie akumulatora o rozmiarach identycznych z obrazem źródłowym. Akumulator wypełniamy, przechodząc po każdym pikselu obrazu, a kiedy napotykamy w tym miejscu krawędź rysujemy w akumulatorze okręg o promieniu \(ir\). Następnie szukamy w akumulatorze miejsc o dużym zagęszczeniu pikseli i na ich podstawie podejmujemy decyzje o istnieniu w tym miejscu okręgu.

Podobny efekt wypełnienia akumulatora możemy uzyskać przy wykorzystaniu filtracji splotowej. Dokonujemy splotu naszego obrazu krawędziowego z maską zawierającą okrąg o promieniu \(ir\). Na poniższym rysunku zaprezentowano przykładowy przebieg działania algorytmu.

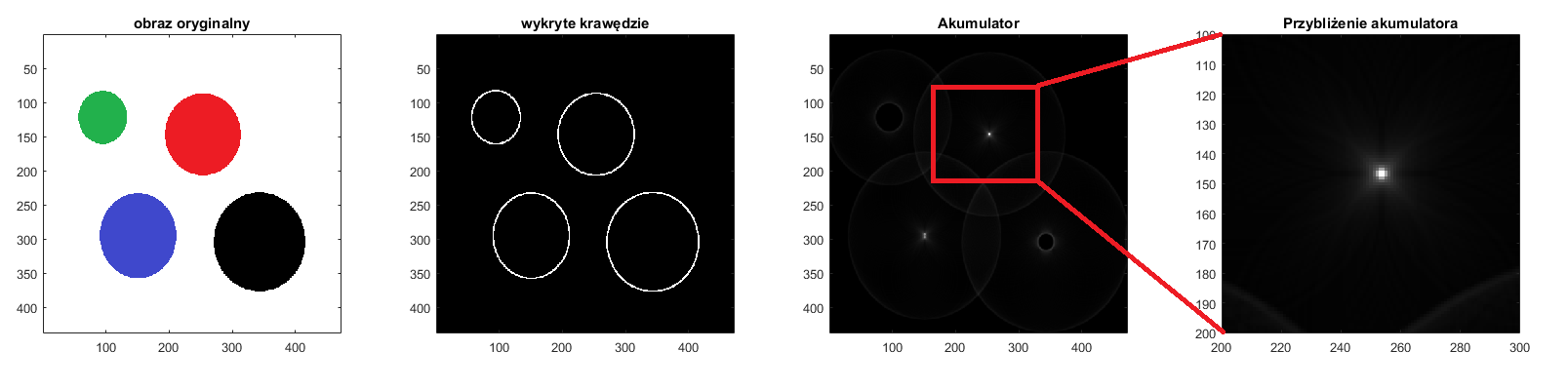
Pierwsza część rysunku zawiera obraz źródłowy, druga to wykryte krawędzie. Cześć trzecia to akumulator wygenerowany dla pewnego \(ir\). Widać kilka jaśniejszych zgrupowań pikseli w miejscach, które są mniej więcej w środkach kół widocznych na oryginalnym obrazie. Proszę zwrócić uwagę, że nie zawsze środki będą miały maksymalną wartość i mogą zajmować kilka pikseli. Należy dlatego znaleźć centra tych plam jako środki okręgów, jako sposób. Do znalezienia tych plam można wykorzystać funkcję:

w, k = np.where(acc >= próg)

Drugi problem “fałszywych” detekcji dotyczy znajdowania okręgów w tym samym miejscu dla kilku kolejnych promieni. Dlatego warto zapisywać tymczasowo wartości odczytane z akumulatora jako “prawdopodobieństwo” bycia okręgiem. Dodatkowo parametr ten można wykorzystać do posegregowania listy naszych okręgu w celu zwrócenia tych \(N\) najbardziej trafnych.

Porada — jak wypełnić maskę

W jaki sposób narysować rastrowy okrąg w rastrze?

Możemy w ty celu wykorzystać funkcje trygonometryczne. Przy założeniu, ze środek naszego okręgu jest w punkcie \((0,0)\) możemy wykorzystać wzór:

\[ \begin{align*} x=R*sin(angle) \\ y=R*cos(angle) \end{align*} \]

Teraz kilka pytań:

• Czy środek naszej maski jest w punkcie \((0,0)\)?
• Jakie format argumentów (jaki typ danych wejściowych) przyjmują funkcje sinus i cosinus?
• Jaki rozmiar (zależny od \(R\)) przyjmie nasza maska? Jak duża musi ona być, żeby cały okrąg się zmieścił.

Samą maskę wypełnia się pętlą po kącie, ale zalecam ustawić krok mniejszy niż \(1^{\circ}\). Polecam dla pewności \(0.05 \text{ rad}\).

Przydatne funkcje Pythona

#######
np.zeros((w, k))
np.sin(angle)
np.cos(angle)
np.arange(start,end,step)
np.pi
np.round().astype('int')
#######
plt.figure(id)
plt.show(block = False)