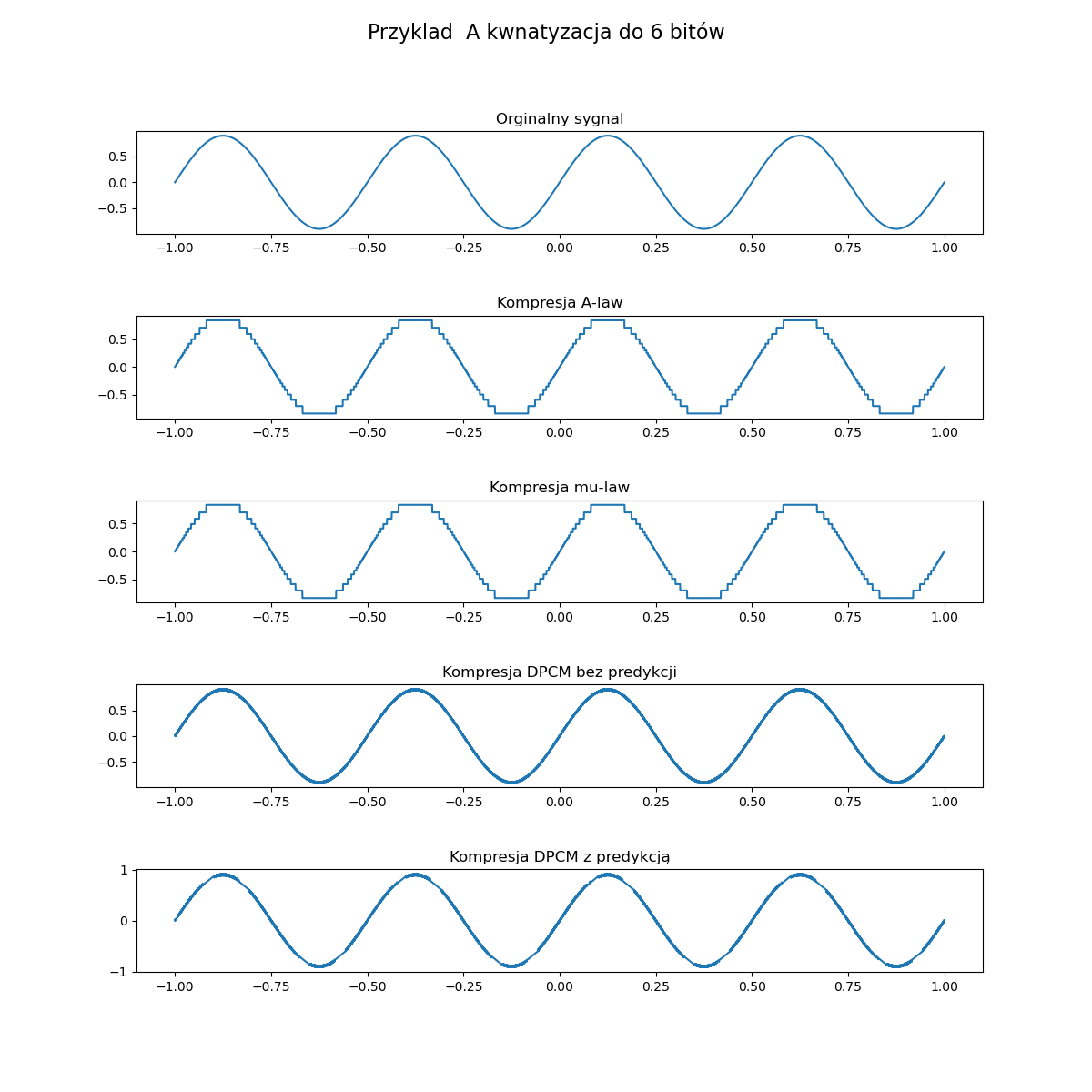
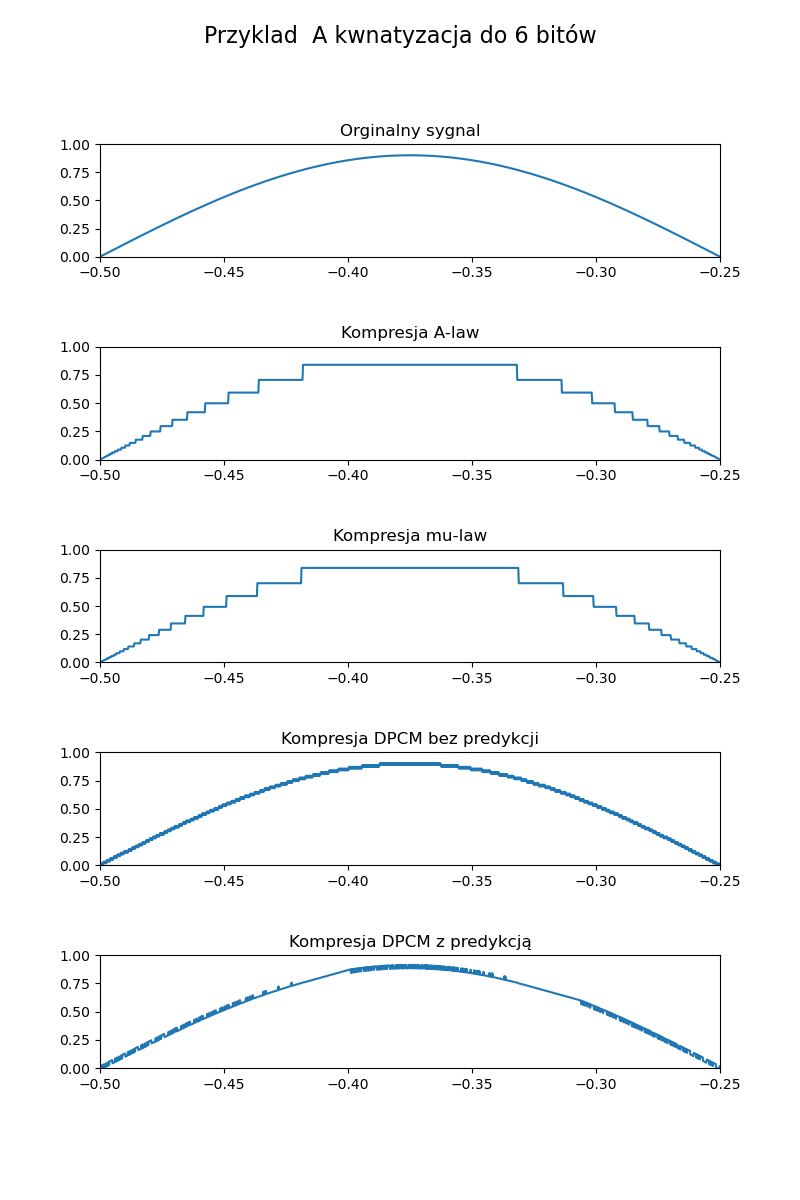
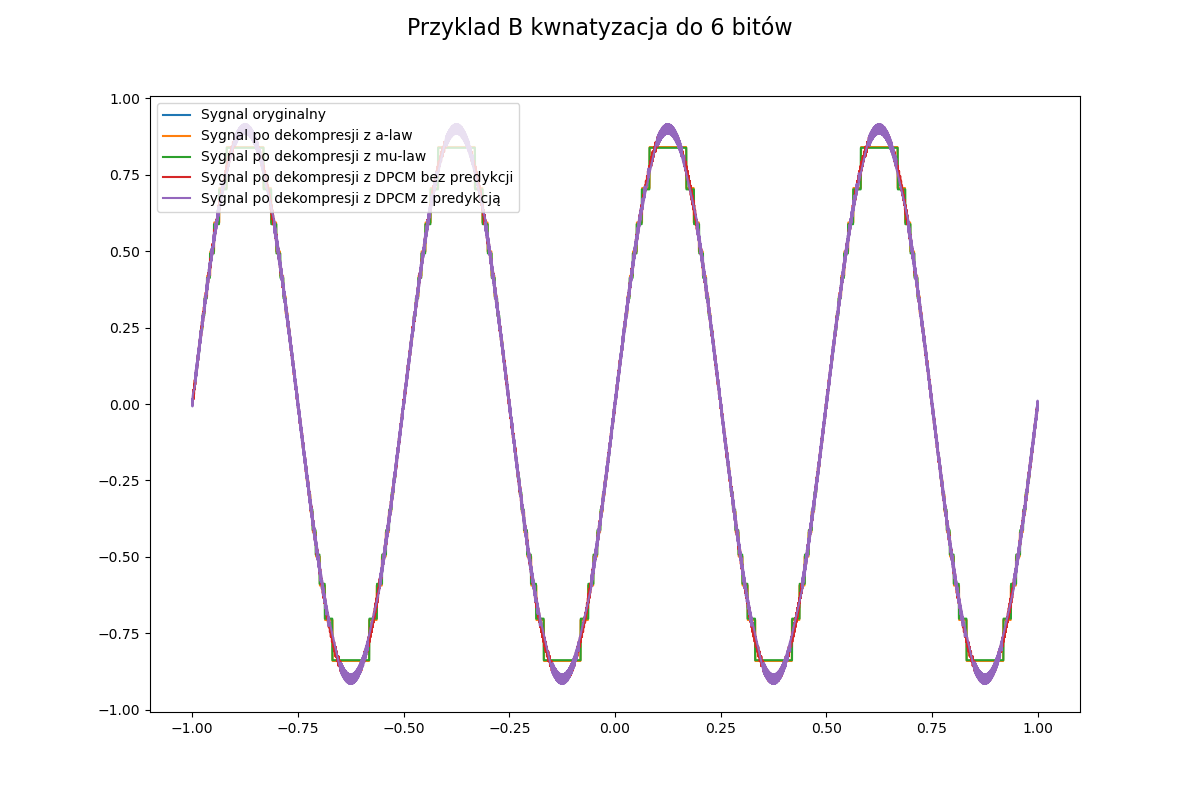
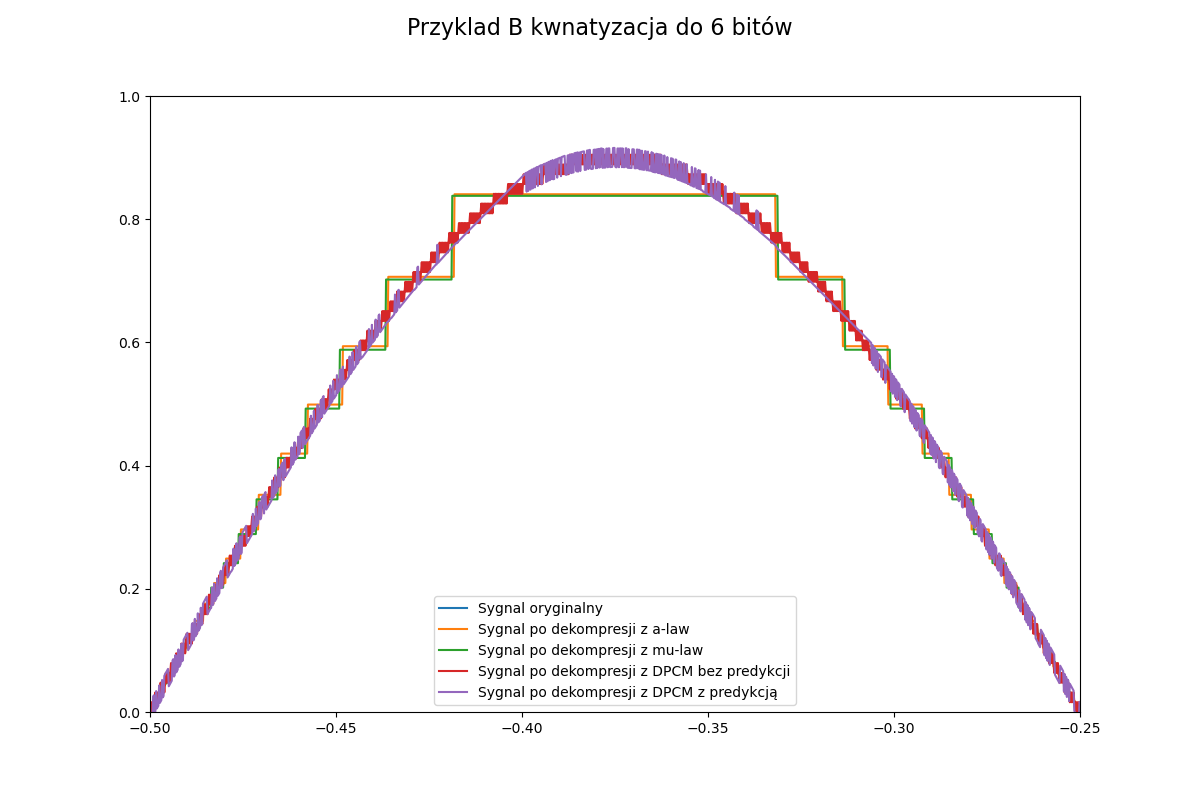
DPCM (ang. Differential Pulse-Code Modulation) – metoda kompresji stratnej przeznaczona głównie dla sygnałów dźwiękowych. Normalny algorytm wykorzystuje predykcję kolejnych wartości sygnałów i koduje jedynie różnice pomiędzy wartością szacowaną a rzeczywistą. My zajmiemy się jego uproszczonymi wersjami, kodującymi zmiany pomiędzy kolejnymi wartościami, zamiast samych wartości. Zmiany te zwykle są mniej dynamiczne niż same wartości sygnału. Schemat kodowania został zaprezentowany na poniższym schemacie.
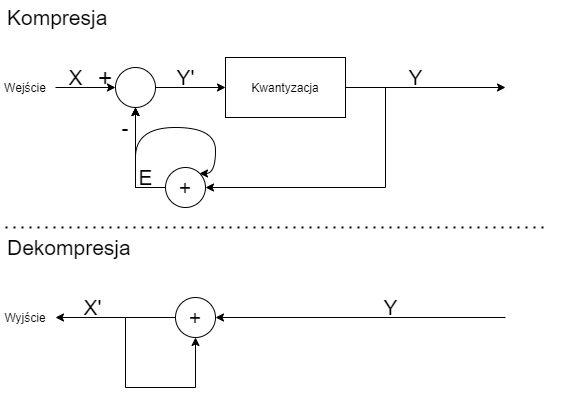
Na początku wyjaśnijmy oznaczenia:
X- sygnał wejściowy,Y'- różnica do zakodowania,Y- zakodowana wartość,E- estymanta/wartość, jaka zostanie odkodowana.
DPCM bez predykcji
Jeżeli potrzebujecie jakieś wcześniejsze wartości początkowe (np. krok -1) zakładamy, że będą one równe \(0\) W każdym kroku algorytmu (dopóki mamy nowe próbki sygnału) będziemy odejmować od bieżącej wartości X wartość estymowaną E, otrzymując w ten sposób wstępną wartość różnicy Y'. Następnie na wartości Y' dokonujemy kwantyzacji (na przykład do wartości 8-bitowej), otrzymując naszą zakodowaną różnicę Y. Następnie dodajemy ją do naszej wartości estymowanej E w celu jej odświeżenia.
Dekompresja odbywa się w podobny sposób. Tu również zakładamy, że X'[0]==Y[0]. Następnie dla każdej kolejnej zakodowanej różnicy dodajemy wartość naszego odtworzonego sygnału z poprzedniego kroku. Należy jednak pamiętać, że nasz sygnał nie jest już zapisany na pierwotnym rozmiarze danych, nie tym po kwantyzacji!!!
Przedstawmy teraz kilka przypadków:
Zakładamy, że chcemy zakodować ciąg \(X=[15,16,20,14,5,10,15,13,11,7,10,11,20,1,23]\). Załóżmy, że zmienna ta będzie zapisana w typie int8 i będziemy stosować dla niej kwantyzacji do konkretniej ilości bitów (7 i 6), przy użyciu naszej standardowej funkcji do kwantyzacji. Poniżej dwa przykłady jak wartości jakie generuje zasza fukcja.:
- Wartości oryginalne: \(X=[-10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]\)
- Wartości po kwantyzacji do 7 bitów: \(X_7=[-9, -9, -7, -7, -5, -5, -3, -3, -1, -1, 0, 0, 2, 2, 4, 4, 6, 6, 8, 8, 10]\)
- Wartości po kwantyzacji do 6 bitów: \(X_6=[-10, -10, -6, -6, -6, -6, -2, -2, -2, -2, 1, 1, 1, 1, 5, 5, 5, 5, 9, 9, 9]\)
W pierwszym przypadku wykorzystamy funkcję do 7-bitów. Zacznijmy od dwóch pierwszych wartości. Kodujemy wartość \(15\), ponieważ w kroku zerowym nasze \(e=0\) nasza różnica będzie wynosić \(Y'=15\). Po kwantyzacji otrzymamy \(Y=K_7(15)=14\), za pomocą tego odświeżymy naszą estymowaną wartość na wyjściu: \(e=X'=Y+e=16+0=16\). Przejdźmy do kodowania kolejnej wartości \(16\). Zaczynamy od wyliczenia różnicy \(Y'=16-14=2\), czyli po kwantyzacji również będziemy mieć \(Y=K_7(2)=2\). Teraz odświeżamy naszą wartość estymowaną \(e=2+16=16\). Reszta kroków została przedstawiona w tabeli.
| Id | \(X\) | \(X-e\) | \(Y'\) | \(Y\) | \(X'=Y+e\) | \(e\) | |||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 15 | 15-0 | 15 | \(\underrightarrow{K_7}\) | 14.0 | 14.0+0 | \(\underrightarrow{e}\) | 14.0 | |
| 1 | 16 | 16-14.0 | 2 | \(\underrightarrow{K_7}\) | 2.0 | 2.0+14.0 | \(\underrightarrow{e}\) | 16.0 | |
| 2 | 20 | 20-16.0 | 4 | \(\underrightarrow{K_7}\) | 4.0 | 4.0+16.0 | \(\underrightarrow{e}\) | 20.0 | |
| 3 | 14 | 14-20.0 | -6 | \(\underrightarrow{K_7}\) | -5.0 | -5.0+20.0 | \(\underrightarrow{e}\) | 15.0 | |
| 4 | 5 | 5-15.0 | -10 | \(\underrightarrow{K_7}\) | -9.0 | -9.0+15.0 | \(\underrightarrow{e}\) | 6.0 | |
| 5 | 10 | 10-6.0 | 4 | \(\underrightarrow{K_7}\) | 4.0 | 4.0+6.0 | \(\underrightarrow{e}\) | 10.0 | |
| 6 | 15 | 15-10.0 | 5 | \(\underrightarrow{K_7}\) | 4.0 | 4.0+10.0 | \(\underrightarrow{e}\) | 14.0 | |
| 7 | 13 | 13-14.0 | -1 | \(\underrightarrow{K_7}\) | -1.0 | -1.0+14.0 | \(\underrightarrow{e}\) | 13.0 | |
| 8 | 11 | 11-13.0 | -2 | \(\underrightarrow{K_7}\) | -1.0 | -1.0+13.0 | \(\underrightarrow{e}\) | 12.0 | |
| 9 | 7 | 7-12.0 | -5 | \(\underrightarrow{K_7}\) | -5.0 | -5.0+12.0 | \(\underrightarrow{e}\) | 7.0 | |
| 10 | 10 | 10-7.0 | 3 | \(\underrightarrow{K_7}\) | 2.0 | 2.0+7.0 | \(\underrightarrow{e}\) | 9.0 | |
| 11 | 11 | 11-9.0 | 2 | \(\underrightarrow{K_7}\) | 2.0 | 2.0+9.0 | \(\underrightarrow{e}\) | 11.0 | |
| 12 | 20 | 20-11.0 | 9 | \(\underrightarrow{K_7}\) | 8.0 | 8.0+11.0 | \(\underrightarrow{e}\) | 19.0 | |
| 13 | 1 | 1-19.0 | -18 | \(\underrightarrow{K_7}\) | -17.0 | -17.0+19.0 | \(\underrightarrow{e}\) | 2.0 | |
| 14 | 23 | 23-2.0 | 21 | \(\underrightarrow{K_7}\) | 20.0 | 20.0+2.0 | \(\underrightarrow{e}\) | 22.0 |
Po całym kodowaniu dostajemy na wyjściu zakodowany łańcuch \(Y=[ 14 , 2, 4, -5, -9 , 4 , 4 , -1 ,-1 , -5 , 2 , 2 , 8, -17, 20]\). Teraz zabieramy się dekodowanie tego łańcucha. Zaczynamy od wartości \(14\), ponieważ nie było kroku -1-go zakładamy, że poprzednia wartość \(X'\) miała wartość \(0\), więc \(X'\) w tym kroku będzie wynosić \(X'=14+0=14\). Kolejna wartość to \(2\), więc nowa wartość to \(X'=2+14=16\). Kontynuacja obliczeń w tabeli.
| Id | \(Y\) | \(Y+X_{-1}\) | \(X'\) |
|---|---|---|---|
| 0 | 14 | 14+0 | 14 |
| 1 | 2 | 2+14 | 16 |
| 2 | 4 | 4+16 | 20 |
| 3 | -5 | -5+20 | 15 |
| 4 | -9 | -9+15 | 6 |
| 5 | 4 | 4+6 | 10 |
| 6 | 4 | 4+10 | 14 |
| 7 | -1 | -1+14 | 13 |
| 8 | -1 | -1+13 | 12 |
| 9 | -5 | -5+12 | 7 |
| 10 | 2 | 2+7 | 9 |
| 11 | 2 | 2+9 | 11 |
| 12 | 8 | 8+11 | 19 |
| 13 | -17 | -17+19 | 2 |
| 14 | 20 | 20+2 | 22 |
Na wyjściu otrzymaliśmy, więc wektor \(X'=[14, 16, 20, 15, 6, 10, 14, 13, 12, 7, 9, 11, 19, 2, 22]\), który jest zbliżony wartościami do \(X=[15,16,20,14,5,10,15,13,11,7,10,11,20,1,23]\).
Przykład dla kwantyzacji do 6 bitów
Teraz przeanalizujmy ten sam przykład, ale dla innej funkcji kwantyzacji do 6-bitów \(K_6(x)\), Poniżej tabele z obliczeniami.
| Id | \(X\) | \(X-e\) | \(Y'\) | \(Y\) | \(X'=Y+e\) | \(e\) | |||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 15 | 15-0 | 15 | \(\underrightarrow{K_6}\) | 13.0 | 13.0+0 | \(\underrightarrow{e}\) | 13.0 | |
| 1 | 16 | 16-13.0 | 3 | \(\underrightarrow{K_6}\) | 1.0 | 1.0+13.0 | \(\underrightarrow{e}\) | 14.0 | |
| 2 | 20 | 20-14.0 | 6 | \(\underrightarrow{K_6}\) | 5.0 | 5.0+14.0 | \(\underrightarrow{e}\) | 19.0 | |
| 3 | 14 | 14-19.0 | -5 | \(\underrightarrow{K_6}\) | -6.0 | -6.0+19.0 | \(\underrightarrow{e}\) | 13.0 | |
| 4 | 5 | 5-13.0 | -8 | \(\underrightarrow{K_6}\) | -6.0 | -6.0+13.0 | \(\underrightarrow{e}\) | 7.0 | |
| 5 | 10 | 10-7.0 | 3 | \(\underrightarrow{K_6}\) | 1.0 | 1.0+7.0 | \(\underrightarrow{e}\) | 8.0 | |
| 6 | 15 | 15-8.0 | 7 | \(\underrightarrow{K_6}\) | 5.0 | 5.0+8.0 | \(\underrightarrow{e}\) | 13.0 | |
| 7 | 13 | 13-13.0 | 0 | \(\underrightarrow{K_6}\) | 1.0 | 1.0+13.0 | \(\underrightarrow{e}\) | 14.0 | |
| 8 | 11 | 11-14.0 | -3 | \(\underrightarrow{K_6}\) | -2.0 | -2.0+14.0 | \(\underrightarrow{e}\) | 12.0 | |
| 9 | 7 | 7-12.0 | -5 | \(\underrightarrow{K_6}\) | -6.0 | -6.0+12.0 | \(\underrightarrow{e}\) | 6.0 | |
| 10 | 10 | 10-6.0 | 4 | \(\underrightarrow{K_6}\) | 5.0 | 5.0+6.0 | \(\underrightarrow{e}\) | 11.0 | |
| 11 | 11 | 11-11.0 | 0 | \(\underrightarrow{K_6}\) | 1.0 | 1.0+11.0 | \(\underrightarrow{e}\) | 12.0 | |
| 12 | 20 | 20-12.0 | 8 | \(\underrightarrow{K_6}\) | 9.0 | 9.0+12.0 | \(\underrightarrow{e}\) | 21.0 | |
| 13 | 1 | 1-21.0 | -20 | \(\underrightarrow{K_6}\) | -18.0 | -18.0+21.0 | \(\underrightarrow{e}\) | 3.0 | |
| 14 | 23 | 23-3.0 | 20 | \(\underrightarrow{K_6}\) | 21.0 | 21.0+3.0 | \(\underrightarrow{e}\) | 24.0 |
| Id | \(Y\) | \(Y+X_{-1}\) | \(X'\) |
|---|---|---|---|
| 0 | 13 | 13+0 | 13 |
| 1 | 1 | 1+13 | 14 |
| 2 | 5 | 5+14 | 19 |
| 3 | -6 | -6+19 | 13 |
| 4 | -6 | -6+13 | 7 |
| 5 | 1 | 1+7 | 8 |
| 6 | 5 | 5+8 | 13 |
| 7 | 1 | 1+13 | 14 |
| 8 | -2 | -2+14 | 12 |
| 9 | -6 | -6+12 | 6 |
| 10 | 5 | 5+6 | 11 |
| 11 | 1 | 1+11 | 12 |
| 12 | 9 | 9+12 | 21 |
| 13 | -18 | -18+21 | 3 |
| 14 | 21 | 21+3 | 24 |
Zestawienie:
- \(X =[15,16,20,14,5,10,15,13,11,7,10,11,20,1,23]\)
- \(X'= [13, 14, 19, 13, 7, 8, 13, 14, 12, 6, 11, 12, 21, 3, 24]\)
- \(Y =[ 13, 1, 5, -6, -6, 1, 5, 1, -2, -6, 5, 1, 9, -18, 21]\)
DPCM z predykcją
Trochę bardziej zaawansowana wersja DPCM zawiera predykcję, czyli wnioskowanie nie tylko na podstawie różnicy i poprzedniego elementu, ale również kilku poprzednich. Istnieją różnego rodzaju mniej lub bardziej zaawansowane predykatory. Najprostszy, jaki będziemy wykorzystywać to średnia ostatnich \(n\) elementów. Czyli zamiast odejmować ostatni estymant będziemy odejmować średnią np. 3 ostatnich sedymentów.
Ogólnie algorytm dla wyliczenia pojedynczego przejścia składa się z kilku kroków:
- Pobieramy wartość do zakodowania \(X_i\)
- Wyliczamy naszą wartość do zakodowania, czyli odejmujemy oczekiwaną wartość z poprzedniego kroku \(E_{i-1}\), więc wykonujemy równanie \(Y_{i}'=X_i-E_{i-1}\)
- Dokonujemy kwantyzacji, czyli dostajemy na wyjście naszej kompresji, czyli \(Y\)
- Wyliczamy wartość, jaką otrzymamy na wyjściu naszego dekodera \(X_i'=Y_i+E_{i-1}\)
- Dokonujemy predykcji na podstawie naszych danych, czyli ostatnich \(n\) wartości \(X_i'\), - przykładowo licząc z nich średnią albo stosując algorytm predykcji liniowej.
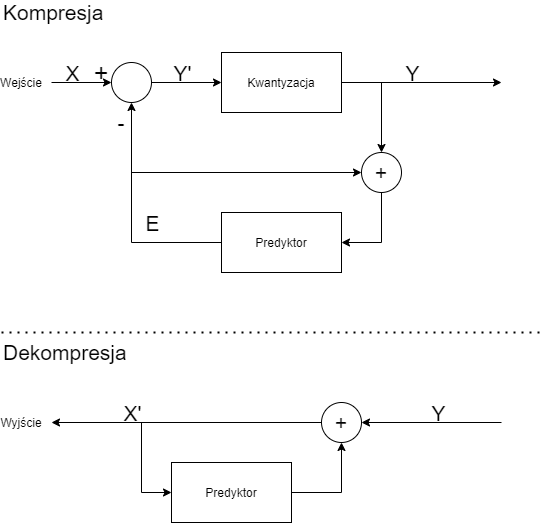
Teraz przejdźmy do przykładów. Zaczniemy od naszego przypadku \(X=[15,16,20,14,5,10,15,13,11,7,10,11,20,1,23]\) i predyktorem średnią z 3 elementów, a wartości będziemy poddawać kwantyzacji do7-bitów. Poniżej przykład bez rzutowania wartości estymowanej na liczbę całkowitą. Dalej również ten sam przykład, ale z zaokrągleniem.
Przykład: DPCM z predykcją na podstawie średniej 3 ostatnich wartości z bez rzutowania jej na liczbę całkowitą
| Id | \(X\) | \(X-e_{i-1}\) | \(Y'\) | \(Y\) | \(X'=Y+e_{-1}\) | \(\overline{X'_{-2\to-0}}\) | \(e_i\) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 15 | 15-0.00 | 15 | \(\underrightarrow{K_7}\) | 14 | 14+0.00=14.00 | \(\overline{[14]}=14.00\) | \(\underrightarrow{e}\) | 14.00 | |
| 1 | 16 | 16-14.00 | 2 | \(\underrightarrow{K_7}\) | 2 | 2+14.00=16.00 | \(\overline{[14,16]}=15.00\) | \(\underrightarrow{e}\) | 15.00 | |
| 2 | 20 | 20-15.00 | 5 | \(\underrightarrow{K_7}\) | 4 | 4+15.00=19.00 | \(\overline{[14,16,19]}=16.33\) | \(\underrightarrow{e}\) | 16.33 | |
| 3 | 14 | 14-16.33 | -2 | \(\underrightarrow{K_7}\) | -1 | -1+16.33=15.00 | \(\overline{[16,19,15]}=16.67\) | \(\underrightarrow{e}\) | 16.67 | |
| 4 | 5 | 5-16.67 | -11 | \(\underrightarrow{K_7}\) | -11 | -11+16.67=5.00 | \(\overline{[19,15, 5]}=13.00\) | \(\underrightarrow{e}\) | 13.00 | |
| 5 | 10 | 10-13.00 | -3 | \(\underrightarrow{K_7}\) | -3 | -3+13.00=10.00 | \(\overline{[15, 5,10]}=10.00\) | \(\underrightarrow{e}\) | 10.00 | |
| 6 | 15 | 15-10.00 | 5 | \(\underrightarrow{K_7}\) | 4 | 4+10.00=14.00 | \(\overline{[ 5,10,14]}=9.67\) | \(\underrightarrow{e}\) | 9.67 | |
| 7 | 13 | 13-9.67 | 3 | \(\underrightarrow{K_7}\) | 2 | 2+9.67=11.00 | \(\overline{[10,14,11]}=11.67\) | \(\underrightarrow{e}\) | 11.67 | |
| 8 | 11 | 11-11.67 | 0 | \(\underrightarrow{K_7}\) | 0 | 0+11.67=11.00 | \(\overline{[14,11,11]}=12.00\) | \(\underrightarrow{e}\) | 12.00 | |
| 9 | 7 | 7-12.00 | -5 | \(\underrightarrow{K_7}\) | -5 | -5+12.00=7.00 | \(\overline{[11,11, 7]}=9.67\) | \(\underrightarrow{e}\) | 9.67 | |
| 10 | 10 | 10-9.67 | 0 | \(\underrightarrow{K_7}\) | 0 | 0+9.67=9.00 | \(\overline{[11, 7, 9]}=9.00\) | \(\underrightarrow{e}\) | 9.00 | |
| 11 | 11 | 11-9.00 | 2 | \(\underrightarrow{K_7}\) | 2 | 2+9.00=11.00 | \(\overline{[ 7, 9,11]}=9.00\) | \(\underrightarrow{e}\) | 9.00 | |
| 12 | 20 | 20-9.00 | 11 | \(\underrightarrow{K_7}\) | 10 | 10+9.00=19.00 | \(\overline{[ 9,11,19]}=13.00\) | \(\underrightarrow{e}\) | 13.00 | |
| 13 | 1 | 1-13.00 | -12 | \(\underrightarrow{K_7}\) | -11 | -11+13.00=2.00 | \(\overline{[11,19, 2]}=10.67\) | \(\underrightarrow{e}\) | 10.67 | |
| 14 | 23 | 23-10.67 | 12 | \(\underrightarrow{K_7}\) | 12 | 12+10.67=22.00 | \(\overline{[19, 2,22]}=14.33\) | \(\underrightarrow{e}\) | 14.33 |
| Id | \(Y\) | \(Y+E_{i-1}\) | \(X'\) | \(\overline{X'_{-2\to0}}\) | \(E_i\) | |
|---|---|---|---|---|---|---|
| 0 | 14 | 14 + 0.00 | 14 | \(\overline{[14]}=14.00\) | \(\underrightarrow{e}\) | 14.00 |
| 1 | 2 | 2 + 14.00 | 16 | \(\overline{[14,16]}=15.00\) | \(\underrightarrow{e}\) | 15.00 |
| 2 | 4 | 4 + 15.00 | 19 | \(\overline{[14,16,19]}=16.33\) | \(\underrightarrow{e}\) | 16.33 |
| 3 | -1 | -1 + 16.33 | 15 | \(\overline{[16,19,15]}=16.67\) | \(\underrightarrow{e}\) | 16.67 |
| 4 | -11 | -11 + 16.67 | 5 | \(\overline{[19,15, 5]}=13.00\) | \(\underrightarrow{e}\) | 13.00 |
| 5 | -3 | -3 + 13.00 | 10 | \(\overline{[15, 5,10]}=10.00\) | \(\underrightarrow{e}\) | 10.00 |
| 6 | 4 | 4 + 10.00 | 14 | \(\overline{[ 5,10,14]}=9.67\) | \(\underrightarrow{e}\) | 9.67 |
| 7 | 2 | 2 + 9.67 | 11 | \(\overline{[10,14,11]}=11.67\) | \(\underrightarrow{e}\) | 11.67 |
| 8 | 0 | 0 + 11.67 | 11 | \(\overline{[14,11,11]}=12.00\) | \(\underrightarrow{e}\) | 12.00 |
| 9 | -5 | -5 + 12.00 | 7 | \(\overline{[11,11, 7]}=9.67\) | \(\underrightarrow{e}\) | 9.67 |
| 10 | 0 | 0 + 9.67 | 9 | \(\overline{[11, 7, 9]}=9.00\) | \(\underrightarrow{e}\) | 9.00 |
| 11 | 2 | 2 + 9.00 | 11 | \(\overline{[ 7, 9,11]}=9.00\) | \(\underrightarrow{e}\) | 9.00 |
| 12 | 10 | 10 + 9.00 | 19 | \(\overline{[ 9,11,19]}=13.00\) | \(\underrightarrow{e}\) | 13.00 |
| 13 | -11 | -11 + 13.00 | 2 | \(\overline{[11,19, 2]}=10.67\) | \(\underrightarrow{e}\) | 10.67 |
| 14 | 12 | 12 + 10.67 | 22 | \(\overline{[19, 2,22]}=14.33\) | \(\underrightarrow{e}\) | 14.33 |
Zestawienie:
- \(X =[15,16,20,14,5,10,15,13,11,7,10,11,20,1,23]\)
- \(X'=[14,16,19,15, 5,10,14,11,11, 7, 9,11,19, 2,22]\)
- \(Y =[ 14, 2, 4, -1,-11, -3, 4, 2, 0, -5, 0, 2, 10,-11, 12]\)
Przykład: DPCM z predykcją na podstawie średniej 3 ostatnich wartości z zaokrągleniem jej do wartości całkowitej
| Id | \(X\) | \(X-e_{i-1}\) | \(Y'\) | \(Y\) | \(X'=Y+e_{-1}\) | \(\overline{X'_{-2\to-0}}\) | \(e_i\) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 15 | 15-0.00 | 15 | \(\underrightarrow{K_7}\) | 14 | 14+0.00=14.00 | \(\overline{[14]}=14.00\) | \(\underrightarrow{e}\) | 14.00 | |
| 1 | 16 | 16-14.00 | 2 | \(\underrightarrow{K_7}\) | 2 | 2+14.00=16.00 | \(\overline{[14,16]}=15.00\) | \(\underrightarrow{e}\) | 15.00 | |
| 2 | 20 | 20-15.00 | 5 | \(\underrightarrow{K_7}\) | 4 | 4+15.00=19.00 | \(\overline{[14,16,19]}=16.33\) | \(\underrightarrow{e}\) | 16.00 | |
| 3 | 14 | 14-16.00 | -2 | \(\underrightarrow{K_7}\) | -1 | -1+16.00=15.00 | \(\overline{[16,19,15]}=16.67\) | \(\underrightarrow{e}\) | 17.00 | |
| 4 | 5 | 5-17.00 | -12 | \(\underrightarrow{K_7}\) | -11 | -11+17.00=6.00 | \(\overline{[19,15, 6]}=13.33\) | \(\underrightarrow{e}\) | 13.00 | |
| 5 | 10 | 10-13.00 | -3 | \(\underrightarrow{K_7}\) | -3 | -3+13.00=10.00 | \(\overline{[15, 6,10]}=10.33\) | \(\underrightarrow{e}\) | 10.00 | |
| 6 | 15 | 15-10.00 | 5 | \(\underrightarrow{K_7}\) | 4 | 4+10.00=14.00 | \(\overline{[ 6,10,14]}=10.00\) | \(\underrightarrow{e}\) | 10.00 | |
| 7 | 13 | 13-10.00 | 3 | \(\underrightarrow{K_7}\) | 2 | 2+10.00=12.00 | \(\overline{[10,14,12]}=12.00\) | \(\underrightarrow{e}\) | 12.00 | |
| 8 | 11 | 11-12.00 | -1 | \(\underrightarrow{K_7}\) | -1 | -1+12.00=11.00 | \(\overline{[14,12,11]}=12.33\) | \(\underrightarrow{e}\) | 12.00 | |
| 9 | 7 | 7-12.00 | -5 | \(\underrightarrow{K_7}\) | -5 | -5+12.00=7.00 | \(\overline{[12,11, 7]}=10.00\) | \(\underrightarrow{e}\) | 10.00 | |
| 10 | 10 | 10-10.00 | 0 | \(\underrightarrow{K_7}\) | 0 | 0+10.00=10.00 | \(\overline{[11, 7,10]}=9.33\) | \(\underrightarrow{e}\) | 9.00 | |
| 11 | 11 | 11-9.00 | 2 | \(\underrightarrow{K_7}\) | 2 | 2+9.00=11.00 | \(\overline{[ 7,10,11]}=9.33\) | \(\underrightarrow{e}\) | 9.00 | |
| 12 | 20 | 20-9.00 | 11 | \(\underrightarrow{K_7}\) | 10 | 10+9.00=19.00 | \(\overline{[10,11,19]}=13.33\) | \(\underrightarrow{e}\) | 13.00 | |
| 13 | 1 | 1-13.00 | -12 | \(\underrightarrow{K_7}\) | -11 | -11+13.00=2.00 | \(\overline{[11,19, 2]}=10.67\) | \(\underrightarrow{e}\) | 11.00 | |
| 14 | 23 | 23-11.00 | 12 | \(\underrightarrow{K_7}\) | 12 | 12+11.00=23.00 | \(\overline{[19, 2,23]}=14.67\) | \(\underrightarrow{e}\) | 15.00 |
| Id | \(Y\) | \(Y+E_{i-1}\) | \(X'\) | \(\overline{X'_{-2\to0}}\) | \(E_i\) | |
|---|---|---|---|---|---|---|
| 0 | 14 | 14 + 0.00 | 14 | \(\overline{[14]}=14.00\) | \(\underrightarrow{e}\) | 14.00 |
| 1 | 2 | 2 + 14.00 | 16 | \(\overline{[14,16]}=15.00\) | \(\underrightarrow{e}\) | 15.00 |
| 2 | 4 | 4 + 15.00 | 19 | \(\overline{[14,16,19]}=16.33\) | \(\underrightarrow{e}\) | 16.00 |
| 3 | -1 | -1 + 16.00 | 15 | \(\overline{[16,19,15]}=16.67\) | \(\underrightarrow{e}\) | 17.00 |
| 4 | -11 | -11 + 17.00 | 6 | \(\overline{[19,15, 6]}=13.33\) | \(\underrightarrow{e}\) | 13.00 |
| 5 | -3 | -3 + 13.00 | 10 | \(\overline{[15, 6,10]}=10.33\) | \(\underrightarrow{e}\) | 10.00 |
| 6 | 4 | 4 + 10.00 | 14 | \(\overline{[ 6,10,14]}=10.00\) | \(\underrightarrow{e}\) | 10.00 |
| 7 | 2 | 2 + 10.00 | 12 | \(\overline{[10,14,12]}=12.00\) | \(\underrightarrow{e}\) | 12.00 |
| 8 | -1 | -1 + 12.00 | 11 | \(\overline{[14,12,11]}=12.33\) | \(\underrightarrow{e}\) | 12.00 |
| 9 | -5 | -5 + 12.00 | 7 | \(\overline{[12,11, 7]}=10.00\) | \(\underrightarrow{e}\) | 10.00 |
| 10 | 0 | 0 + 10.00 | 10 | \(\overline{[11, 7,10]}=9.33\) | \(\underrightarrow{e}\) | 9.00 |
| 11 | 2 | 2 + 9.00 | 11 | \(\overline{[ 7,10,11]}=9.33\) | \(\underrightarrow{e}\) | 9.00 |
| 12 | 10 | 10 + 9.00 | 19 | \(\overline{[10,11,19]}=13.33\) | \(\underrightarrow{e}\) | 13.00 |
| 13 | -11 | -11 + 13.00 | 2 | \(\overline{[11,19, 2]}=10.67\) | \(\underrightarrow{e}\) | 11.00 |
| 14 | 12 | 12 + 11.00 | 23 | \(\overline{[19, 2,23]}=14.67\) | \(\underrightarrow{e}\) | 15.00 |
Zestawienie:
- \(X =[15,16,20,14,5,10,15,13,11,7,10,11,20,1,23]\)
- \(X'=[14,16,19,15, 6,10,14,12,11, 7,10,11,19, 2,23]\)
- \(Y =[ 14, 2, 4, -1,-11, -3, 4, 2, -1, -5, 0, 2, 10,-11, 12]\)
Inne metody predykcji
- Średnia geometryczna (
scipy.stats.mstats.gmean) - może wymagać obudowania własną funkcją - Średnia harmoniczna (
scipy.stats.mstats.hmean) - może wymagać obudowania własną funkcją - Mediana
- Predykcja liniowa \[\begin{aligned} p=1\qquad:&\qquad\hat{x}(n)=1x(n-1)\\ p=2\qquad:&\qquad\hat{x}(n)=2x(n-1)-1x(n-2)\\ p=3\qquad:&\qquad\hat{x}(n)=3x(n-1)-3x(n-2)+1x(n-3)\\ p=4\qquad:&\qquad\hat{x}(n)=4x(n-1)-6x(n-2)+4x(n-3)-1x(n-4)\\ \end{aligned}\]
- Regresja liniowa
Przykład: DPCM z predykcją na podstawie predykcji liniowej dla n do 4 elementów
Wzory są powyżej. Dla rzeczywistych sygnałów działa lepiej.
| Id | \(X\) | \(X-e_{i-1}\) | \(Y'\) | \(Y\) | \(X'=Y+e_{-1}\) | \(f(X'_{-3\to-0})\) | \(e_i\) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 15 | 15-0.00 | 15 | \(\underrightarrow{K_7}\) | 14 | 14+0.00=14.00 | \(f([14])=14.00\) | \(\underrightarrow{e}\) | 14.00 | |
| 1 | 16 | 16-14.00 | 2 | \(\underrightarrow{K_7}\) | 2 | 2+14.00=16.00 | \(f([14,16])=12.00\) | \(\underrightarrow{e}\) | 12.00 | |
| 2 | 20 | 20-12.00 | 8 | \(\underrightarrow{K_7}\) | 8 | 8+12.00=20.00 | \(f([14,16,20])=14.00\) | \(\underrightarrow{e}\) | 14.00 | |
| 3 | 14 | 14-14.00 | 0 | \(\underrightarrow{K_7}\) | 0 | 0+14.00=14.00 | \(f([14,16,20,14])=26.00\) | \(\underrightarrow{e}\) | 26.00 | |
| 4 | 5 | 5-26.00 | -21 | \(\underrightarrow{K_7}\) | -21 | -21+26.00=5.00 | \(f([16,20,14, 5])=-5.00\) | \(\underrightarrow{e}\) | -5.00 | |
| 5 | 10 | 10–5.00 | 15 | \(\underrightarrow{K_7}\) | 14 | 14+-5.00=9.00 | \(f([20,14, 5, 9])=7.00\) | \(\underrightarrow{e}\) | 7.00 | |
| 6 | 15 | 15-7.00 | 8 | \(\underrightarrow{K_7}\) | 8 | 8+7.00=15.00 | \(f([14, 5, 9,15])=47.00\) | \(\underrightarrow{e}\) | 47.00 | |
| 7 | 13 | 13-47.00 | -34 | \(\underrightarrow{K_7}\) | -33 | -33+47.00=14.00 | \(f([ 5, 9,15,14])=12.00\) | \(\underrightarrow{e}\) | 12.00 | |
| 8 | 11 | 11-12.00 | -1 | \(\underrightarrow{K_7}\) | -1 | -1+12.00=11.00 | \(f([ 9,15,14,11])=-9.00\) | \(\underrightarrow{e}\) | -9.00 | |
| 9 | 7 | 7–9.00 | 16 | \(\underrightarrow{K_7}\) | 16 | 16+-9.00=7.00 | \(f([15,14,11, 7])=13.00\) | \(\underrightarrow{e}\) | 13.00 | |
| 10 | 10 | 10-13.00 | -3 | \(\underrightarrow{K_7}\) | -3 | -3+13.00=10.00 | \(f([14,11, 7,10])=8.00\) | \(\underrightarrow{e}\) | 8.00 | |
| 11 | 11 | 11-8.00 | 3 | \(\underrightarrow{K_7}\) | 2 | 2+8.00=10.00 | \(f([11, 7,10,10])=32.00\) | \(\underrightarrow{e}\) | 32.00 | |
| 12 | 20 | 20-32.00 | -12 | \(\underrightarrow{K_7}\) | -11 | -11+32.00=21.00 | \(f([ 7,10,10,21])=-13.00\) | \(\underrightarrow{e}\) | -13.00 | |
| 13 | 1 | 1–13.00 | 14 | \(\underrightarrow{K_7}\) | 14 | 14+-13.00=1.00 | \(f([10,10,21, 1])=63.00\) | \(\underrightarrow{e}\) | 63.00 | |
| 14 | 23 | 23-63.00 | -40 | \(\underrightarrow{K_7}\) | -39 | -39+63.00=24.00 | \(f([10,21, 1,24])=-106.00\) | \(\underrightarrow{e}\) | -106.00 |
| Id | \(Y\) | \(Y+E_{i-1}\) | \(X'\) | \(f(X'_{-3\to-0})\) | \(E_i\) | |
|---|---|---|---|---|---|---|
| 0 | 14 | 14 + 0.00 | 14 | \(f([14])=14.00\) | \(\underrightarrow{e}\) | 14.00 |
| 1 | 2 | 2 + 14.00 | 16 | \(f([14,16])=12.00\) | \(\underrightarrow{e}\) | 12.00 |
| 2 | 8 | 8 + 12.00 | 20 | \(f([14,16,20])=14.00\) | \(\underrightarrow{e}\) | 14.00 |
| 3 | 0 | 0 + 14.00 | 14 | \(f([14,16,20,14])=26.00\) | \(\underrightarrow{e}\) | 26.00 |
| 4 | -21 | -21 + 26.00 | 5 | \(f([16,20,14, 5])=-5.00\) | \(\underrightarrow{e}\) | -5.00 |
| 5 | 14 | 14 + -5.00 | 9 | \(f([20,14, 5, 9])=7.00\) | \(\underrightarrow{e}\) | 7.00 |
| 6 | 8 | 8 + 7.00 | 15 | \(f([14, 5, 9,15])=47.00\) | \(\underrightarrow{e}\) | 47.00 |
| 7 | -33 | -33 + 47.00 | 14 | \(f([ 5, 9,15,14])=12.00\) | \(\underrightarrow{e}\) | 12.00 |
| 8 | -1 | -1 + 12.00 | 11 | \(f([ 9,15,14,11])=-9.00\) | \(\underrightarrow{e}\) | -9.00 |
| 9 | 16 | 16 + -9.00 | 7 | \(f([15,14,11, 7])=13.00\) | \(\underrightarrow{e}\) | 13.00 |
| 10 | -3 | -3 + 13.00 | 10 | \(f([14,11, 7,10])=8.00\) | \(\underrightarrow{e}\) | 8.00 |
| 11 | 2 | 2 + 8.00 | 10 | \(f([11, 7,10,10])=32.00\) | \(\underrightarrow{e}\) | 32.00 |
| 12 | -11 | -11 + 32.00 | 21 | \(f([ 7,10,10,21])=-13.00\) | \(\underrightarrow{e}\) | -13.00 |
| 13 | 14 | 14 + -13.00 | 1 | \(f([10,10,21, 1])=63.00\) | \(\underrightarrow{e}\) | 63.00 |
| 14 | -39 | -39 + 63.00 | 24 | \(f([10,21, 1,24])=-106.00\) | \(\underrightarrow{e}\) | -106.00 |
Zestawienie:
- \(X =[15,16,20,14,5,10,15,13,11,7,10,11,20,1,23]\)
- \(X'=[14,16,20,14, 5, 9,15,14,11, 7,10,10,21, 1,24]\)
- \(Y =[ 14, 2, 8, 0,-21, 14, 8,-33, -1, 16, -3, 2,-11, 14,-39]\)
Przykładowy kod
DPCM bez predykcji
def DPCM_compress(x,bit): y=np.zeros(x.shape) e=0 for i in range(0,x.shape[0]): y[i]=kwant(x[i]-e,bit) e+=y[i] return yDPCM z predykcją
def DPCM_compress(x,bit,predictor,n): y=np.zeros(x.shape) xp=np.zeros(x.shape) e=0 for i in range(0,x.shape[0]): y[i]=kwant(x[i]-e,bit) xp[i]=y[i]+e idx=(np.arange(i-n,i,1,dtype=int)+1) idx=np.delete(idx,idx<0) e=predictor(xp[idx]) return yPredyktor bez predykcji:
def no_pred(X): return X[-1]
Jak testować?
Jeżeli chodzi o testowanie to błędy najłatwiej zaobserwować na fragmencie sinusa:
x=np.linspace(-1,1,1000)
y=0.9*np.sin(np.pi*x*4)