Re-sampling to operacja polegająca na zmianie częstotliwości próbkowania. Wyróżniamy dwa rodzaje re-samplingu:

up-sampling -sztuczne zwiększanie częstotliwości próbkowania,
down-sampling — obniżanie częstotliwości próbkowania.

Na zajęciach będziemy zajmować się tylko prostymi metodami zmniejszania częstotliwości próbkowania, a dokładnie dwoma prostymi metodami: Decymacją oraz Interpolacją. Pamiętajmy jednak, że redukcja częstotliwości próbkowania zmniejsza nam również ilość częstotliwości, jakie przenosi sygnał.

Decymacja

Najprostszy i najmniej złożony obliczeniowo proces redukcji częstotliwości próbkowania. Polega na wzięciu co n-tej próbki sygnału. Przykładowo, jeżeli z sygnału o częstotliwości 48 kHz weźmiemy co 10 próbkę dostaniemy nowy sygnał o częstotliwości próbkowania 4800 Hz, a gdy weźmiemy co drugą próbkę to nowy sygnał będzie miał częstotliwość 24000 Hz. Wadą tego rozwiązania jest możliwość zmiany częstotliwości tylko o wielokrotności liczb całkowitych. Oprócz sygnału po decymacji warto zwracać również nową częstotliwość próbkowania, żeby pamiętać, że ona również uległa zmianie (\(Fs/n\)). Podpowiedź programistyczna:

x[::n]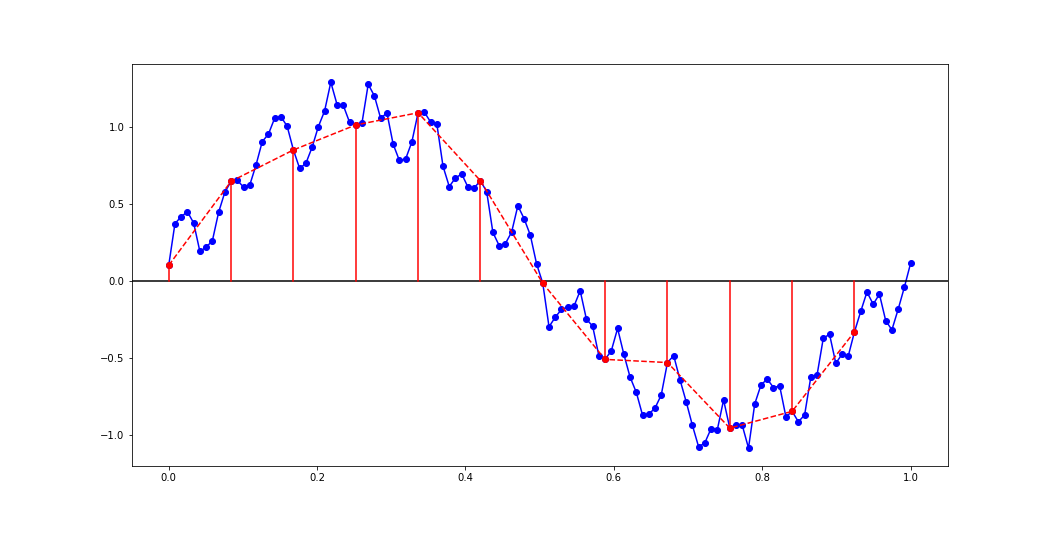

Przykład decymacji sygnału

Interpolacja liniowa i nieliniowa

Drugim sposobem jest wykorzystanie interpolacji liniowej i nieliniowej. Pozwala ona w dowolny sposób przeliczyć częstotliwości próbkowania w dowolny sposób. Czyli funkcje interpolacyjne pozwalają wyznaczyć wartości funkcji dla dowolnych nowych punktów w czasie, które nie muszą się bezpośrednio pokrywać z już posiadanymi. Ta metoda pozwala nam przekształcić sygnał z 48 kHz na sygnał 44.1 kHz. Od strony kodowej będziemy wykorzystywać bibliotekę scipy. Zakładamy, że mamy nasze dane źródłowe: y będzie naszym sygnałem, a x będzie czasem odpowiadającym poszczególnym wartościom sygnału. Analogicznie musimy stworzyć czasy x1, jakie będą odpowiadać wartością nowego sygnału. Na podstawie naszych danych źródłowych należy stworzyć wpierw funkcję interpolującą (metoda interp1d), a następnie wywołać ją na nowych punktach czasowych.

from scipy.interpolate import interp1d

metode_lin=interp1d(x,y)
metode_nonlin=interp1d(x,y, kind='cubic')

y_lin=metode_lin(x1).astype(y.dtype)
y_nonlin=metode_nonlin(x1).astype(y.dtype)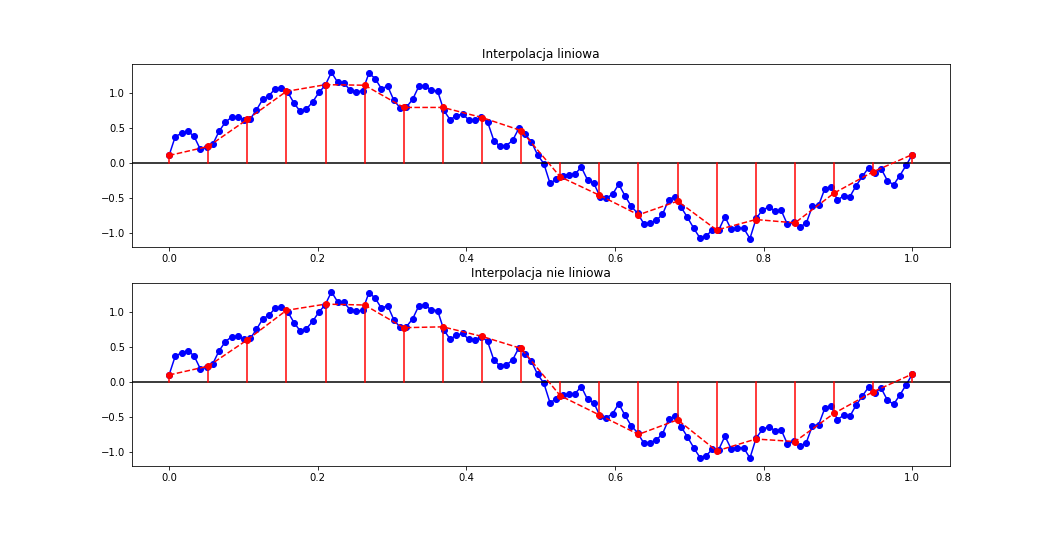

Przykład interpolacji sygnału

Są dwa sposoby na generowanie \(x\)/\(t\) oraz \(x_1\)/\(t_1\) zakładamy, że \(N\) to ilość próbek oryginalnego sygnału a \(N_1\) to ilość próbek nowego sygnału:

Wybieramy przestrzeń numerów próbek:

x=np.linspace(0,N,N)
x1=np.linspace(0,N,N1)

Wybieramy przestrzeń czasową (łatwiejsze do zrozumienia):
```
t=np.linspace(0,N/Fs,N)
t1=np.linspace(0,N/Fs,N1)
```

Uwaga końcowa

Po raz n-ty przypominam: pamiętajcie, że jakakolwiek zmiana próbkowania zmienia wam jego częstotliwość (Fs), więc trzeba pamiętać o jej zmianie we wzorach na wyświetlanie widma oraz we funkcjach odtwarzania/zapisu dźwięku.