Kwantyzacja to nazwa grupy przekształceń, które w założeniu zmniejszają dokładność zapisanego sygnału. Operacja kwantyzacji jest nieodwracalna i powoduje utratę informacji. W naszym przypadku będziemy starali się zapisywać dane przy użyciu mniejszej ilości bitów.
Kwantyzacja sygnału dostarcza nam pewnych problemów z wyświetlaniem/odtwarzaniem naszych sygnałów. Większość metod, jakie mamy dostępne, interpretuje tym zmiennych, jeżeli będziemy wyświetlać obraz na uint8, to jeżeli nasze wartości będą zapisane na 4-bitach (\(0,1,\dots,15\)) to obraz będzie bardzo ciemny. Podobnie, jeżeli obraz będzie zapisany na float, a wartości będą większe niż \(1\) obraz będzie cały biały. Z dźwiękiem jest nawet gorzej, ponieważ w przypadku małych wartości dźwięk będzie bardzo cichy lub bardzo zniekształcony. Z tych powodów często będziemy zwykle symulować zmniejszenie rozdzielczości bitowej przy jednoczesnym zachowaniu domyślnego zakresu wartości.
Wartości typów mniejszych niż 16 bitów nie jest odtwarzana automatycznie przez bibliotekę sounddevice, a tylko zmiana typu na obsługiwany nie zapewni nam tej możliwości, ponieważ otrzymane sygnały będą za ciche, by można było je usłyszeć. Wymaga to od nas zwiększenia wartości sygnału po kwantyzacji tak, aby wypełniały one przestrzeń wartości w podobnym zakresie, ale występowała tylko kluczowa ilość wartości.
Symulowanie rozdzielczości bitowej
Redukcja rozdzielczość bitowej polega na zmniejszeniu ilości bitów, na jakich zostały zapisane dane. Dla uproszczenia naszych działań wszystkie wykorzystywane w tej części typy danych (zarówno te rzeczywiste, jak i sztucznie przez nas tworzone) będą oparte o wartości całkowite (int). Domyślnie wszystkie pliki dźwiękowe powinniśmy wczytywać w formacie np.int32, to znaczy, że wszystkie wartości, jakie są w nich zawarte powinny zawierać się w przedziale \(<-2147483648,2147483647>\). Jest to zależne od tego, że nasza liczba jest 32-bitowa, czyli możemy zapisać za jej pomocą \(2^{32}=4294967296\) wartości. Tak samo dla uproszczenia będziemy zakładać, że liczna zmiennoprzecinkowa (float), na 32 bitach też będzie przechowywać dokładnie tyle wartości — w praktyce jest to większa liczba wartości, ale mniejszą dokładnością. Za pomocą Pythona możemy dostać te wartości graniczne zakresu dla każdego ze wbudowanych typów za pomocą funkcji:
np.iinfo(data.dtype).min
np.iinfo(data.dtype).maxCo więcej, jeżeli chcemy sprawdzić ilość unikalnych wartości, mamy w naszym zakresie możemy policzyć to, za pomocą komendy:
np.unique().sizeWygodnym rozwiązaniem jest również sprawdzenie, czy obsługiwana przez nas zmienna jest konkretnego typu przy wykorzystaniu komend:
np.issubdtype(data.dtype,np.integer)
np.issubdtype(data.dtype,np.floating)Symulowanie rozdzielczości bitowej można dokonywać na co najmniej dwa sposoby:
Przy wykorzystaniu wzorów na rzutowanie typów, z odpowiednim zaokrąglaniem:
[Wzrór](?cat=M&l=G_01/CONVEQ)- Rzutowanie z oryginalnego zakresu na zakres o zmniejszonej rozdzielczości bitowej (np.
float32do “uint5”), - zaokrąglenie wartości (
np.round), - rzutowanie z nowego zakresu na pierwotny zakres (“uint5” do
float32).
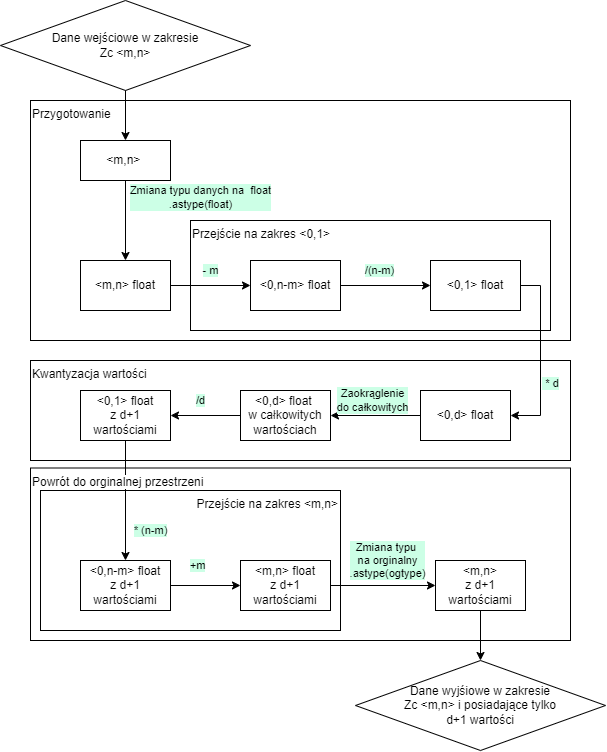
- Rzutowanie z oryginalnego zakresu na zakres o zmniejszonej rozdzielczości bitowej (np.
Wygenerowanie wartości oczekiwanych w danym zakresie, a zastąpienie każdej wartości sygnału najbliższą jej wartością z oczekiwanego ciągu (Podobnie jak w przypadku
colorFitz laboratoriów z ditheringiem).
Uwaga do metody pierwszej: Należy pamiętać, że pisząc funkcję dokonującą redukcję symulacji warto dostosować ją do automatycznego znajdowania wartości \(m\) oraz \(n\). Dla zmiennych całkowitych (int oraz uint) wartości te są pobierane z zakresu zmiennej. Natomiast dla zmiennych zmiennoprzecinkowych (float) jest to zależne od typu zawartości.
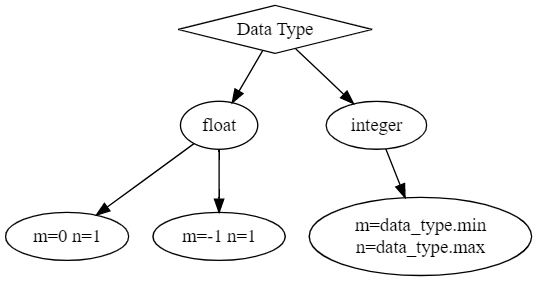
Sugerowana struktura funkcji kwantyzującej powinna wyglądać tak:
def Kwant(data,bit):
d=... #oblicz ilość wartości/ maksymalną wartość całkowitą
if np.issubdtype(data.dtype,np.floating)
#co jeżeli float?
else
#co jeżeli integer?
DataF=Data.astype(float)
# kwantyzacja na DataF
return DataF.astype(data.dtype)Przykładowe wartości dla zakresów rozdzielczości bitowej dla różnych zakresów wartości zamieszczone w tabelce poniżej.
| Ilość bitów | Ilość wartości | uint8 |
\(<0,1>\) float |
\(<-1,1>\) float |
|---|---|---|---|---|
| 1 - bity | \(2^1=2\) | \([0,255]\) | \([0,1]\) | \([-1,1]\) |
| 2 - bity | \(2^2=4\) | \([ 0, 85, 170, 255]\) | \([0. , 0.33, 0.67, 1. ]\) | \([-1. , -0.33, 0.33, 1. ]\) |
| 3 - bity | \(2^3=8\) | \([ 0, 36, 73, 109, 146, 182, 219, 255]\) | \([0. , 0.14, 0.29, 0.43, 0.57, 0.71, 0.86, 1. ]\) | \([-1. , -0.71, -0.43, -0.14, 0.14, 0.43, 0.71, 1. ]\) |
| 4 - bity | \(2^4=16\) | \([ 0, 17, 34, 51, \dots, 204, 221, 238, 255]\) | \([0. , 0.07, 0.13, 0.2 , \dots , 0.8 , 0.87, 0.93, 1. ]\) | \([-1. , -0.87, -0.73, -0.6 , \dots ,0.6 , 0.73, 0.87, 1. ]\) |
Jak testować oraz najczęstsze błędy
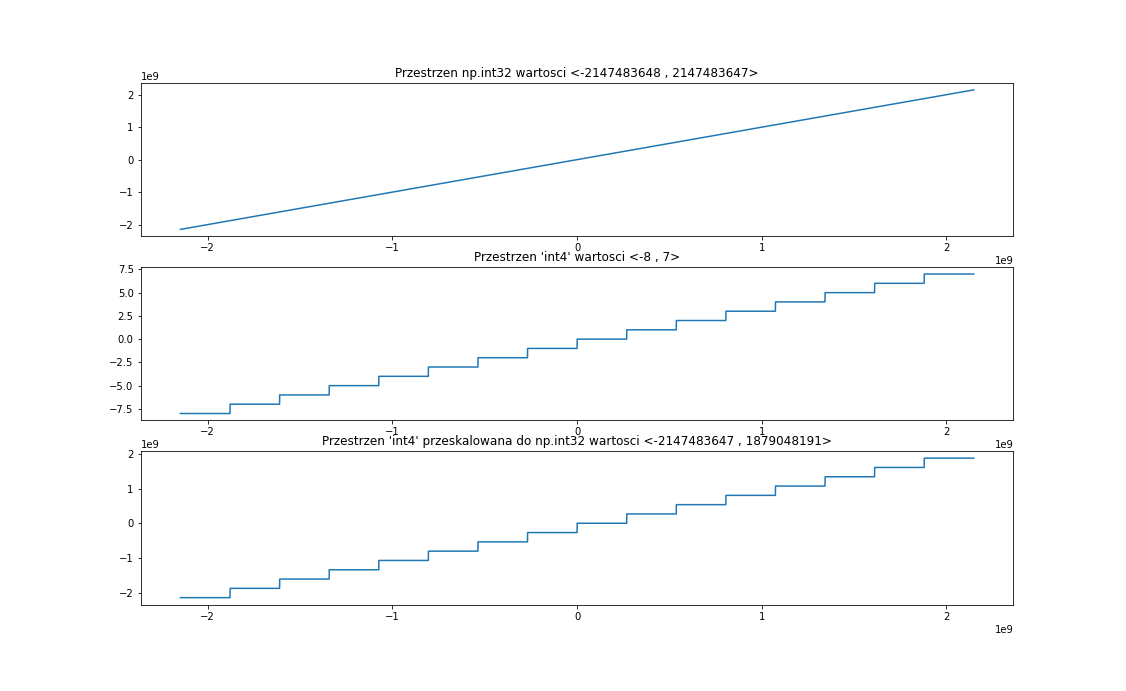
Najłatwiej testować na podstawie wszelkie przedstawienia wizualizować sobie za pomocą wykresów na osi OX powinien być zakres początkowy, a na osi OY zakres po przekształceniu. Jeżeli coś będzie nie tak, to bardzo łatwo w sposób zauważcie to na wykresach.
Zakresy startowe można wygenerować za pomocą funkcji np.linspace. Przykładowo:
np.round(np.linspace(0,255,255,dtype=np.uint8))
np.round(np.linspace(np.iinfo(np.int32).min,np.iinfo(np.int32).max,1000,dtype=np.int32))
np.linspace(-1,1,10000)Interaktywane przykłady
Najczęściej pojawiające się błędy (ta część będzie rozszerzana, jak tylko będą się pojawiały przykłady)
- Problemy z zaokrąglaniem — można je zobaczyć jako nierówne segmenty na wykresie lub jako pojedyncze wartości na końcach zakresu,
- Próba wyliczania nowych wartości (przy użyciu metody 1) bez przesunięcia się na pozytywną cześć zakresu przed rzutowaniem — można to zobaczyć jako dużo dłuższy przedział na środku wykresu.