Każdy zapisany cyfrowo obraz jest obrazem rzeczywistości (dla obrazów generowanych na komputerze jest to rzeczywistość cyfrowa), na którym przeprowadzono pewien proces próbkowania. Próbkowanie jest przeprowadzone z pewną rozdzielczością i ona określa nam dokładność naszego obrazu. W ramach zajęć będziemy starać się zmienić tę dokładność, przy pomocy prostych metod i sprawdzić ich wpływ na informacje w nim zawarte. Wykorzystamy kilka prostych technik służących powiększaniu i zmniejszaniu rozmiaru obrazu.

Uwagi wstępne

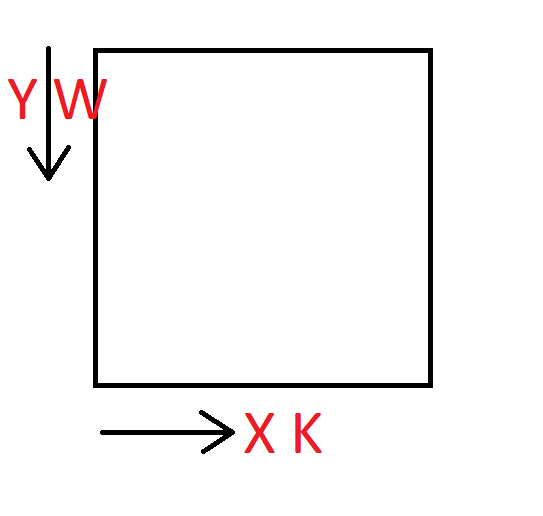
Uwaga 1 Obraz zapisany w pamięci posiada współrzędne, w innej kolejności niż jesteście do tego przyzwyczajeni. Pierwsza współrzędna określa wiersze, czyli współrzędną Y, natomiast druga określa kolumnę, czyli współrzędną X. Warto o tym pamiętać, bo pomoże wam to uniknąć zamieszania z niektórymi algorytmami. Poniżej rysunek poglądowy.

Uwaga 2 Wszystkie prezentowane tu rozwiązania i algorytmy są przedstawiane przy założeniu, że pracujemy na obrazie w skali odcieni szarości. W ramach zajęć będziecie implementować również warianty tych rozwiązań, które działają również dla obrazów RGB. Obrazy te różnią się ilością wymiarów, więc trzeba albo pisać kod w sposób pozwalający na wywołanie ich na kilku warstwach (Python oraz Pakiet NumPy pozwalają to robić w sposób prosty), albo sprawdzić rodzaj przetwarzany obrazu, to można do tego wykorzystać zapytanie:

if (len(OG.shape)<3): 
    ### grayscale
else:
    ### RGB

Uwaga 3 Proszę pamiętać, że plt.imshow() domyślnie zakłada, że typy danych mają domyślne zakresy wyświetlania. Przykładowo obrazy na float, powinny być w zakresie \(<0,1>\). Jeżeli tak nie jest może być potrzeba rzutowania ich na inne typy przykładowo .astype(np.uint8).

Uwaga 4 Przy zmianie rozmiaru obrazu będziemy przekazywać wartość o skalowaniu. Może być ona przekazana na dwa sposoby:

• Procentowej: \(100\) obraz pozostaje bez zmian, \(50\) będzie o połowę mniejszy, a \(150\) będzie o połowę większy.
• Jako stosunek skalowania: \(1\) obraz pozostaje bez zmian, \(0.5\) będzie o połowę mniejszy, a \(1.5\) będzie o połowę większy.

Należy pamiętać, żeby utworzyć nową zmienną, do której będziemy potem zapisywać nowe wartości pikseli.

Uwaga 5 Najwygodniej wygenerować nową siatkę pikseli przy użyciu funkcji np.linspace(od,do,ile), gdzie początek i koniec są zawsze wymiarami naszego obrazu modyfikowanego. Natomiast ilość jest zależna od rozmiaru naszego obrazu na wyjściu.

Metody skalowania obrazu — Powiększanie i pomniejszania

Algorytmy powiększania obrazu służą zwiększeniu dostępnych pikseli w ramach naszego obrazu i teoretycznie zwiększają nam ilość danych. Omówimy dwie takie metody. Wszystkie przykłady działania tych algorytmów w formie graficznej zostaną przedstawione na końcu sekcji im poświęconej.

Oba algorytmy opisują założenia działania dla przykładowego piksela nowego obrazu w ramach jego najbliższego otoczenia. W przypadku powiększania obrazu gęstość pikseli w nowym obrazie powinna być większa dla tej samej powierzchni. Jak widać na poniższym rysunku nasz nowy piksel \(P\) jest umieszczony w otoczeniu 4 pikseli \(Q\). Zakładamy, że na etapie wyliczania wartości naszego nowego piksela znamy już jego pozycję w przestrzeni starego obrazu.

Pamiętajmy również, że zawsze musimy podjąć jakieś decyzje dotyczące pikseli brzegowych i uwzględnić to jakoś w obliczeniach.

Metoda najbliższego sąsiada

Metoda najbliższego sąsiada jest, jedną z najłatwiejszych metod polega na znalezieniu, który z pikseli \(Q\) jest najbliżej piksela \(P\) i on przekazuje mu swoją wartość. Wygodnym tu rozwiązaniem wydaje się zastosowanie funkcji zaokrąglających np.round.

Rozpatrzmy przykład jednowymiarowy, czyli jedeną współrzędną naszego obrazu. Zacznijmy od określenia rozmiarów wejściowych i wyjściowych naszych danych. Załóżmy, że nasz obraz wejściowy (jednowymiarowy), będzie miał \(10\) elementów i będziemy go powiększać o \(333\%\), czyli nasz obraz wyjściowy (jednowymiarowy), będzie miał rozmiar \(10*333\%=10*\dfrac{333}{100}=33.3\). W praktyce są to \(34\) elementy, żeby otrzymać wartość całkowitą zaokrągloną w górę można wykorzycać funkcję np.ceil(...).astype(int).

Kolejnym krokiem jest wygenerowanie miejsc, gdzie piksele naszego powiększonego obrazu mniej więcej znajdują się w przestrzeni naszego obrazu. Posłużymy się w tym celu zestawem komend:

X=np.linspace(0,10-1,34)
print(X)
for i in range(0,34):
    print(X[i])

Przeanalizujmy sobie pewien konkretny przypadek z naszego wektora pod współrzędną o indeksie \(12\), czyli \(xx=3.27\). W tym przypadku w naszym nowym obrazie pod współrzędną \(12\) należy wpisać wartość ze starego obrazu spod współrzędnej o indeksie \(3\). Ponieważ, gdy zaokrąglimy naszą wartość z \(xx\) otrzymamy taką wartość.

Interpolacja dwuliniowa

Ta metoda jest trochę bardziej złożona. Wartość dla piksela \(P\) wyliczamy na podstawie wartości pikseli \(Q\) i jego odległości do nich. Z pełnym założeniem, teorią i sposobem wyliczania go można zapoznać się tutaj. W naszym przypadku możemy poczynić pewne założenia i uprościć całe rozwiązanie. Gdy założymy, że nasze piksele \(Q\) są równomiernie rozłożone na współrzędnych \((0,0)\),\((0,1)\),\((1,0)\) oraz \((1,1)\), a odległości punktu \(P\) od wierzchołka \((0,0)\) zapiszemy jako \(x\) i \(y\). Będą one miały wartości \(x\in<0,1>\) oraz \(y\in<0,1>\), czyli będą tak naprawdę częścią dziesiętną naszej współrzędnej (\(0,....\)). Możemy wtedy założyć, że wartość interpolowana może być zbliżona do średniej ważonej, gdzie powierzchnie obszarów przeciwległych stanowią wagi dla poszczególnych wierzchołków, to znaczy wagę dla wierzchołka \(Q_{22}\) stanowi obszar pomiędzy \(Q_{11}\), a \(P\). Można to zapisać za pomocą poniższego wzoru, gdzie \(f(x,y)\) to wartość nowego piksela w punkcie \((x,y)\):

\[ f(x,y)\approx f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xy \]

Spróbujemy również rozpatrzyć nasz jednowymiarowy przypadek jednowymiarowy z poprzedniej części, czyli nasze \(xx=3.636\). Na ten postawie wyliczamy wartości \(x_1=3\) (zaokrąglenie w dół) oraz \(x_2=4\) (zaokrąglenie w górę). Teraz potrzebujemy jeszcze wartości \(x\), czyli odległości do lewego piksela w naszym obrazie będzie to dla nas \(xx-x_1=3.636-3=0.636\). Mamy teraz wszystkie dane potrzebne do obliczenia wartości dla naszego nowego piksela. W tym celu wykorzystamy uproszoną wersję powyższego wzoru. Będzie to wyglądać mniej więcej tak:

\[ f(x_1)(1-x)+f(x_2)(x) = f(3)(1-0.636)+f(4)(0.636)= f(3)(0.364)+f(4)(0.636) \]

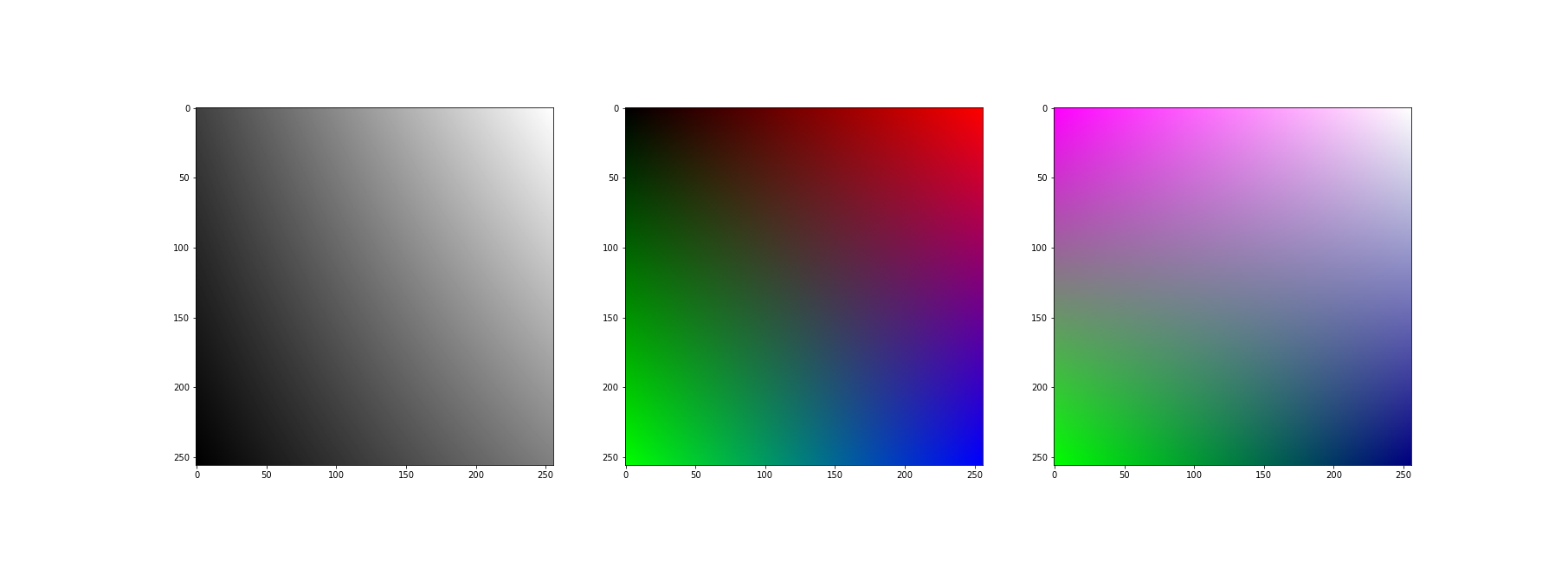
Przykłady różnych płaszczyzn interpolacji dla wartości pikseli zaprezentowano poniżej:

Przykłady działania funkcji zwiększających rozmiar obrazu:

Przykład testowy dla obu metod:

img= np.zeros((3,3,3),dtype=np.uint8)
img[1,1,:]=255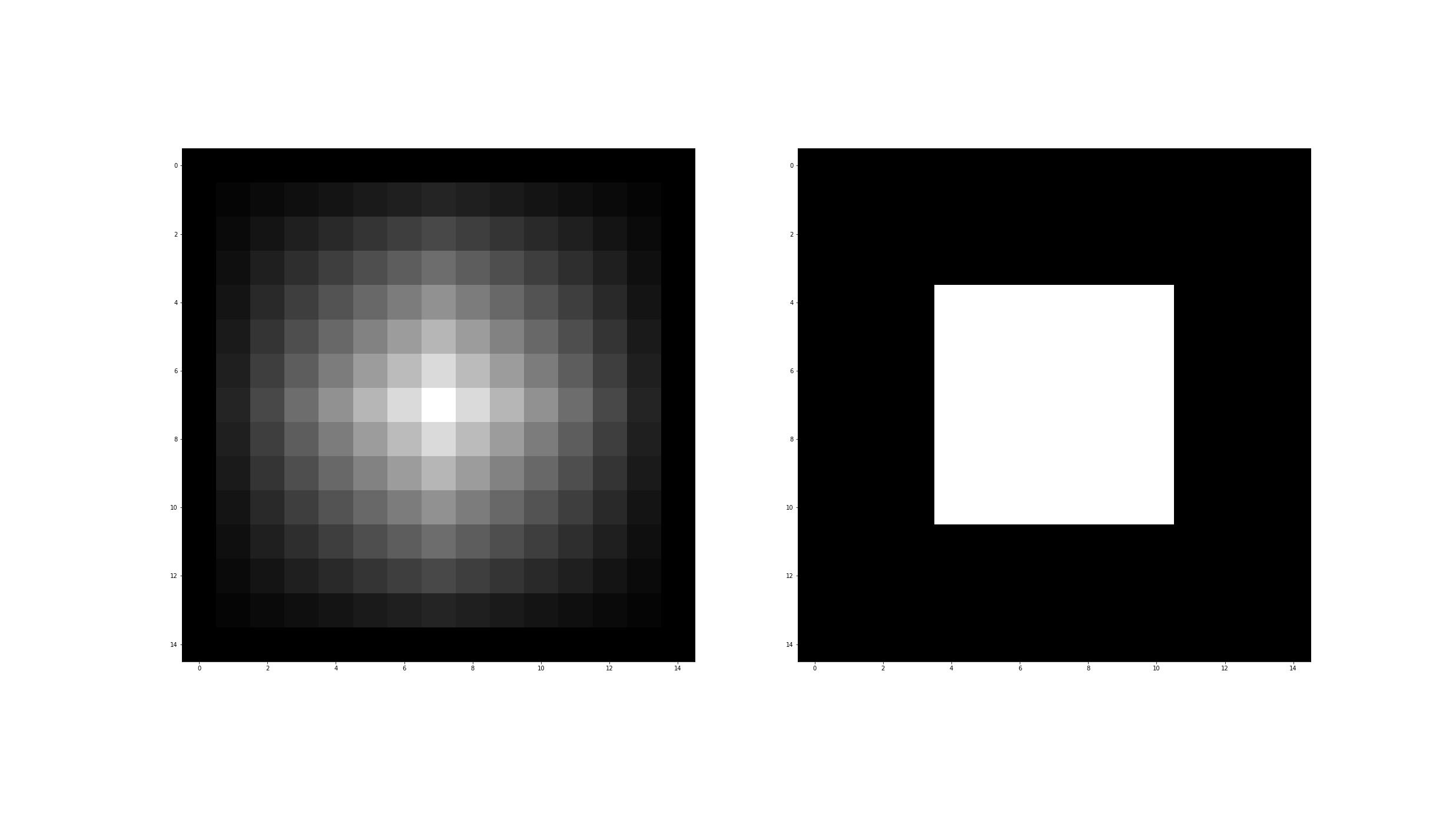

Zmniejszanie obrazu

Do zmniejszania rozdzielczości obrazu możemy wykorzystywać różne metody. Zmniejszenie obrazu ma na celu zmniejszenie jego miejsca w pamięci oraz zmniejszeniu liczby detali. W poprawny sposób napisane algorytmy służące do powiększania obrazu również powinny się do tego celu nadawać. Dodatkowo wykorzystywać można algorytmy analizujące otoczenie danego piksela.

Zastosowanie mediany, średniej lub średniej ważonej do wyliczenia wartości nowego piksela

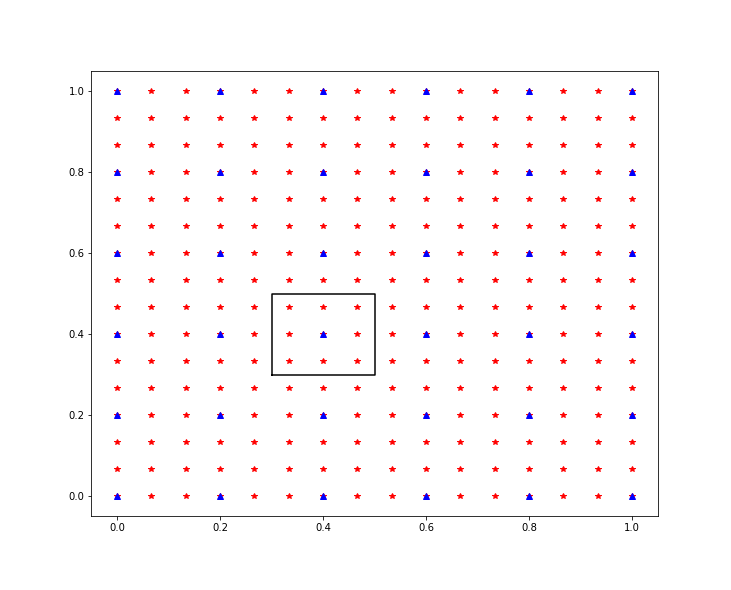
W przypadku tego zestawu metod będziemy analizować otoczenie nowo powstałego piksela. W przypadku zmniejszania rozmiaru naszego obrazu ilość pikseli obrazu oryginalnego przypadającą na obszar, jaki będzie reprezentować nasz nowy piksel będzie \(\geq1\). Przykładowe rozmieszczenie nowych (niebieskie) i oryginalnych (czerwone) pikseli zaprezentowano na rysunku poniżej. Na czarno zaznaczono przykładowe otoczenie nowego piksela. Pragnę tylko zaznaczyć, że w większości przypadków otoczenie nie będzie raczej tak równe i symetryczne, zwłaszcza w przypadku krawędzi obrazu. Otoczenie naszego nowego piksela może być wyznaczane dynamicznie (na podstawie odległości do sąsiadujących nowych pikseli) lub zakładając maksymalne sąsiedztwo (np. 3x3, 5x5) i ewentualnie zmniejszając je w przypadku, gdy nie jesteśmy go w całości wykorzystać.

Współrzędne dla naszego pomniejszonego obrazu wyliczamy w ten sam sposób jak w przypadku powiększania obrazu. Załóżmy, że pomniejszamy nasz 10-elementowy wektor do \(33\%\), czyli będziemy mieli \(4\) elementy.

xx=np.linspace(0,10,4)

Na podstawie tych wartości możemy wyliczać otoczenia. Jak już wspomniane było wcześniej mamy dwa rodzaje otoczenia:

• Statyczne — generowane ze stałym krokiem np.

  ix=np.round(xx[i]+np.arange(-3,4))

• Dynamiczne — generowane dynamicznie na podstawie odległości pomiędzy punktami np. (można rozszerzyć o dodatkowe np.ceil, żeby rozszerzyć to otoczenie).

  if i>0:
      x1=-(xx[i]-xx[i-1])/2
  else:
      x1=0
  if i<len(xx)-1:   
      x2=(xx[i+1]-xx[i])/2+1
  else:
      x2=0
  ix=np.round(xx[i]+np.arange(x1,x2)).astype(int)

W obu przypadkach należy pamiętać, że granice tego przedziału będą jednostronne na granicach przedziałów. Czyli trzeba dodać if-y lub clip, który nas zabezpieczy przed wyjściem poza zakres \(<0,m>\).

ix=ix.clip(0,m)

Teraz mamy zakres naszych nowych współrzędnych możemy wyodrębnić nasz lokalny fragment:

X_fragment= X[ix[0]:ix[-1]]

Jak na podstawie otoczenia wyliczyć wartość nowego piksela? Do dyspozycji mamy kilka podstawowych operacji do przetestowania:

• Średnia np.mean,
• Mediana np.median,
• Średnia ważona \(\dfrac{\sum{O * W}}{\sum{W}}\) (przydatne funkcje np.sum, np.multiply).

Uwaga dotycząca średniej ważonej — średnia ważona działa tylko wtedy, gdy wagi są różne dla różnych pól. Jeżeli wszystkie wagi są identyczne, to nie jest to średnia ważona tylko zwykła średnia. Rozpatrujemy też średnią w ramach warstwy, jeżeli wartości na jednej warstwie są identyczne, to też jest to średnia, a nie średnia ważona.

Wszystkie te opcje działają na fragmencie będącym otoczeniem. O tym, czym jest fragment i jak go wyodrębnić było na pierwszych zajęciach. Przy średniej ważonej pamiętajcie o dwóch informacjach:

1. Nie zawsze będziecie mieć idealne symetryczne otoczenie i często część wag może być pominięta, więc:
2. Pamiętajcie, żeby zawsze dzielić uzyskany wynik przez sumę wszystkich użytych wag.

Jeżeli nie wiecie jak dobrać wagi, to możecie wygenerować je w sposób losowy.

Przykłady działania algorytmów:

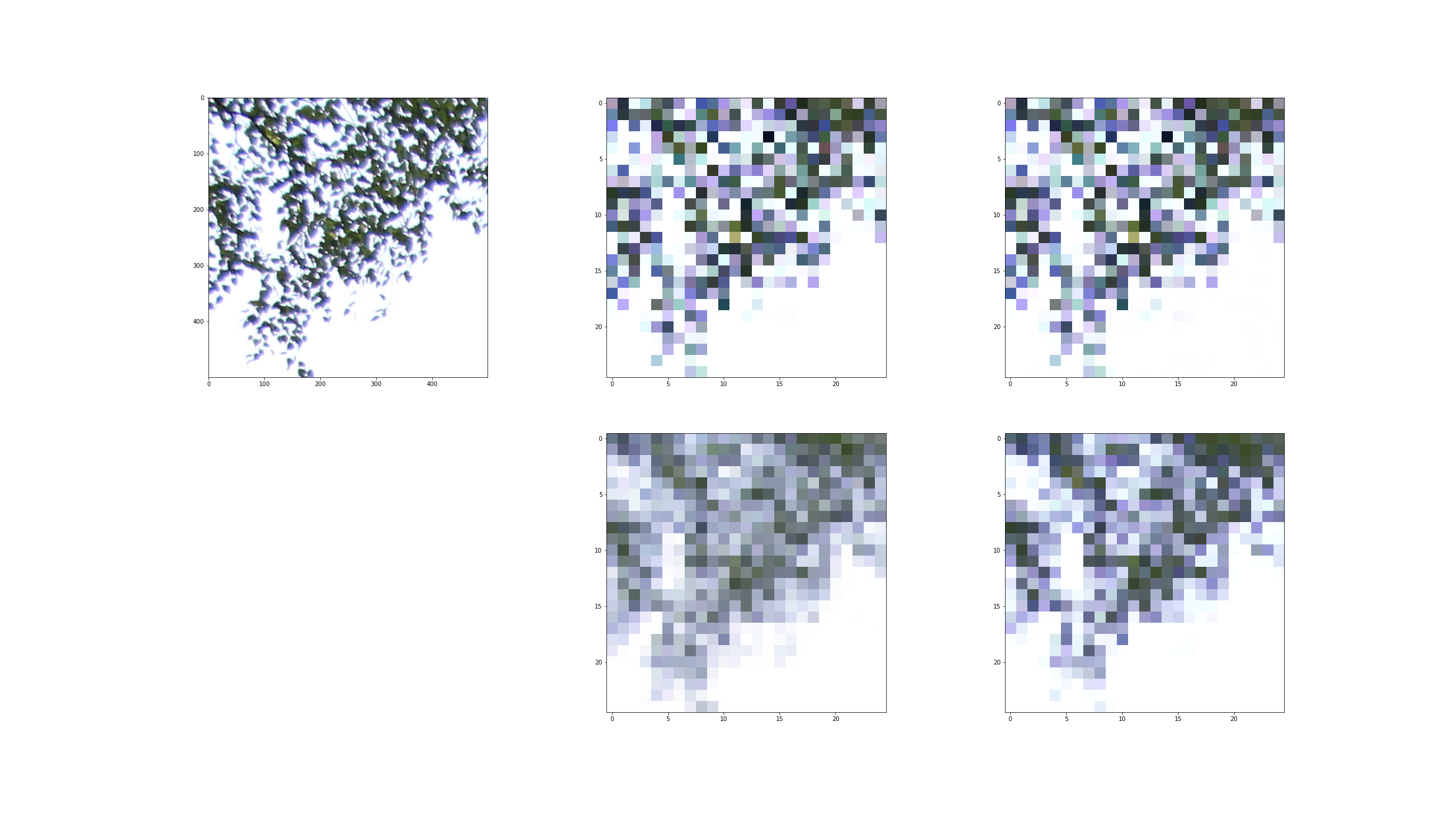
Obrazy kolorowe

W przypadku obrazów kolorowych postępujemy w ten sam sposób jak przy obrazach w skali odcieni szarości. W niektórych przypadkach część operacji wykona się bez żadnych dodatkowych zmian w kodzie, w pozostałych przypadkach powtarzamy jednak każdą z tych operację 3-krotnie, czyli po jednym wykonaniu na każdej warstwie.

Przydatne funkcje do sprawdzenia w dokumentacji

np.linspace()
np.zeros()
.astype(np.uint8)
round()
np.sum()
np.ceil()
np.around()
np.sum()
np.multiply()