Operacje morfologiczne to zestaw operacji dla obrazów binarnych (\(0\) lub \(1\)), które badają otoczenie pod kątem logicznym. Każda z operacji zakłada, że mamy obraz binarny (\(I\)) oraz element strukturyzujący (\(B\)) opisujący otoczenie. Oba mogą być dowolnego rozmiaru (ale zakładamy, rozmiar \(B\) nie będzie większy od rozmiaru \(I\))

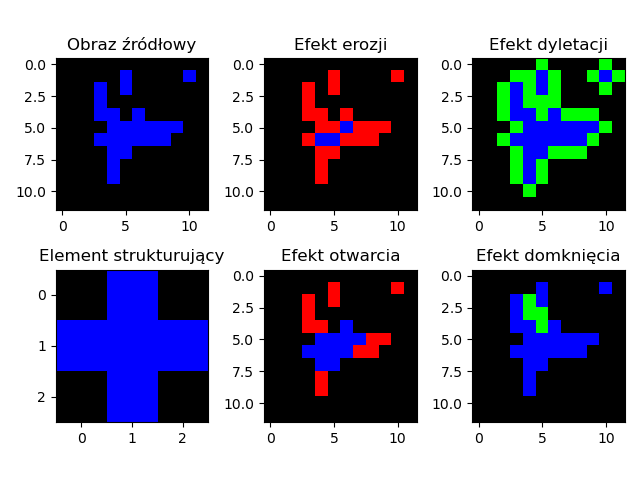
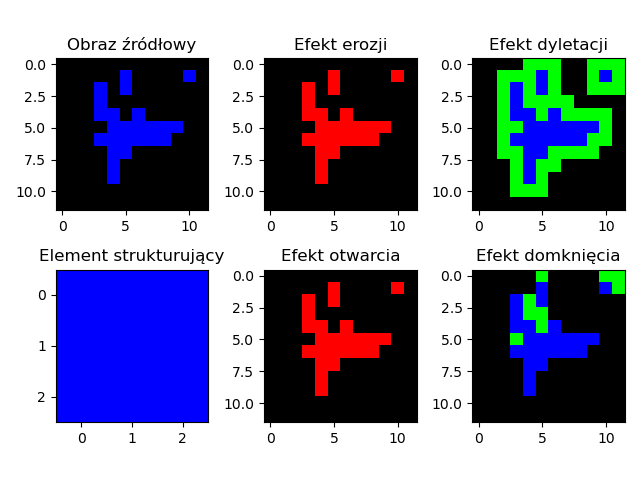
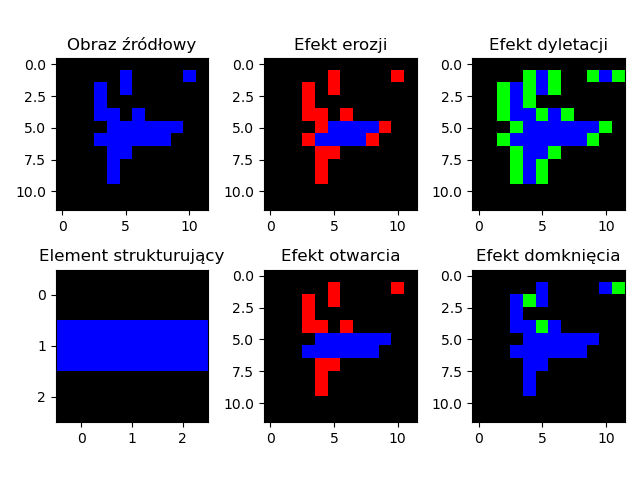
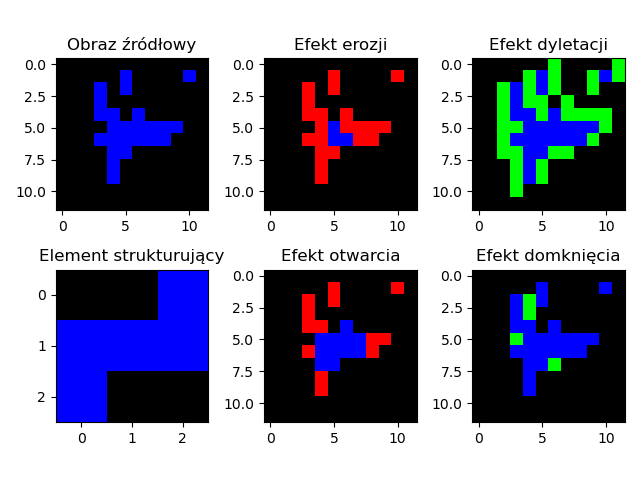
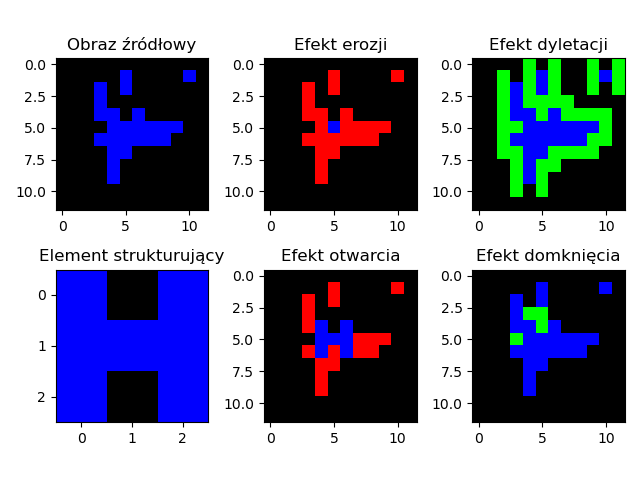
Dylatacja \(I \oplus B\) Dylatacja, czyli rozszerzanie. Jeżeli chociaż jeden piksel z w obszarze \(B\) ma wartość równą \(1\) to na wyjściu operacji dostajemy \(1\) w przeciwnym wypadku dostajemy \(0\).
Erozja \(I \ominus B\) Erozja, czyli zwężanie. Jeżeli chociaż jeden piksel z w obszarze \(B\) ma wartość równą \(0\) to na wyjściu operacji dostajemy \(0\). Jeżeli wszystkie piksele w otoczeniu \(B\) będą równe \(1\) to na wyjściu dostajemy \(1\).
Otwarcie \(I \circ B = (I \ominus B)\oplus B\) Otwarcie morfologiczne jest równoważne nałożeniu operacji dylatacji na wynik erozji obrazu pierwotnego.
Domknięcie \(I \bullet B = (I \oplus B)\ominus B\) Operacja domknięcia morfologicznego jest równoważne nałożeniu operacji erozji na wynik dylatacji obrazu pierwotnego.

Przykłady operacji morfologicznych dla różnych elementów strukturyzujących

Jak przerobić funkcję to filtracji splotowej na funkcję do operacji morfologicznych?

Do przerobienia potrzeba dwóch kroków:

Pierwszy krok wybranie wartości dla otoczenia dla naszego elementu strukturyzującego (maski):
```
    O=fragment[np.logical_and(fragment,mask)]
```

Wykonujemy sprawdzenie naszej funkcji dylatacji lub erozji:

    # dylatacja
    (O==1).any()
    # erozja
    (O==1).all()

Przykładowe elementy strukturyzujące

Kwadrat \[ \begin{array}{|c|c|c|}\hline 1 & 1 & 1\\ \hline 1 & \color{green}{1} & 1\\ \hline 1 & 1 & 1\\ \hline \end{array} \qquad \begin{array}{|c|c|c|c|c|}\hline 1 & 1 &1 & 1 & 1\\ \hline 1 & 1 &1 & 1 & 1\\ \hline 1 & 1 & \color{green}{1} & 1 & 1\\ \hline 1 & 1 &1 & 1 & 1\\ \hline 1 & 1 &1 & 1 & 1\\ \hline \end{array} \qquad \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & \color{green}{1} & 1 & 1 &1 & 1 & 1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline \end{array} \]
Dysk \[ \begin{array}{|c|c|c|}\hline \color{gray}{0} & 1 & \color{gray}{0}\\ \hline 1 & \color{green}{1} & 1\\ \hline \color{gray}{0} & 1 & \color{gray}{0}\\ \hline \end{array} \qquad \begin{array}{|c|c|c|c|c|}\hline \color{gray}{0} & 1 &1 & 1 & \color{gray}{0}\\ \hline 1 & 1 &1 & 1 & 1\\ \hline 1 & 1 & \color{green}{1} & 1 & 1\\ \hline 1 & 1 &1 & 1 & 1\\ \hline \color{gray}{0} & 1 &1 & 1 & \color{gray}{0}\\ \hline \end{array} \qquad \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline \color{gray}{0} & \color{gray}{0} &\color{gray}{0} & \color{gray}{0} & \color{gray}{0} & 1 & 1 & 1 & 1 & 1 &\color{gray}{0} & \color{gray}{0} &\color{gray}{0} & \color{gray}{0} & \color{gray}{0}\\ \hline \color{gray}{0} & \color{gray}{0} &\color{gray}{0} & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &\color{gray}{0} & \color{gray}{0} & \color{gray}{0} \\ \hline \color{gray}{0} & \color{gray}{0} &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & \color{gray}{0} & \color{gray}{0} \\ \hline \color{gray}{0} & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & \color{gray}{0} \\ \hline \color{gray}{0} & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & \color{gray}{0} \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & \color{green}{1} & 1 & 1 &1 & 1 & 1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline 1 & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & 1 \\ \hline \color{gray}{0} & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & \color{gray}{0} \\ \hline \color{gray}{0} & 1 &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & 1 & \color{gray}{0} \\ \hline \color{gray}{0} & \color{gray}{0} &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & \color{gray}{0} & \color{gray}{0} \\ \hline \color{gray}{0} & \color{gray}{0} &1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &1 & \color{gray}{0} & \color{gray}{0} \\ \hline \color{gray}{0} & \color{gray}{0} &\color{gray}{0} & 1 & 1 & 1 & 1 & 1 & 1 & 1 &1 & 1 &\color{gray}{0} & \color{gray}{0} & \color{gray}{0} \\ \hline \color{gray}{0} & \color{gray}{0} &\color{gray}{0} & \color{gray}{0} & \color{gray}{0} & 1 & 1 & 1 & 1 & 1 &\color{gray}{0} & \color{gray}{0} &\color{gray}{0} & \color{gray}{0} & \color{gray}{0}\\ \hline \end{array} \]