Uproszczony algorytm DCD - Dominant Color Descriptor

Uproszczony algorytm DCD w przeciwieństwie do pełnego algorytmu nie dokonuje analizy statystycznej danych wejściowych, ale dokonuje kwantyzacji obrazu w przestrzeni HSV z określonymi wagami a następnie ich dyskretyzacji.

Napisana funkcja wygeneruje na podstawie obrazu wejściowego listę N kolorów dominujących w HSV wraz z procentowymi ilościami oraz znormalizowany histogram zawierający N wartości niezerowych z domyślnych 72. Domyślnie N powinno być równe 8. Sam algorytm składa się z następujących kroków:

• Konwersja z RGB do HSV (można wykorzystać funkcję z OpenCV),
• Kwantyzacja poszczególnych kanałów,
• Utworzenie histogramu trójwymiarowego (8x3x3),
• Linearyzacja histogramu z 3D do 1D zgodnie z regułą podana na wykładzie (\(H^{(1D)} (9h + 3s + v) = H^{(3D)} (h,s,v)\) przy założeniu że indeksujemy od 0 !) - czyli zamieniamy 8x3x3 na 72x1,
• Wybór N kolorów dominujących,
• Przygotowanie danych wyjściowych:
  • Przygotowanie listy kolorów wraz ich procentowym występowaniem,
  • Wyzerowanie pozostałych wartości w histogramie a następnie ich normalizacja (do jedności na podstawie sumy wszystkich wartości histogramu po zerowaniu).

Domyślne wagi jakie wykorzystujemy przedstawiono poniżej, ale można je modyfikować jeżeli uznacie to za słuszne. Zakładane zakresy wartości dla HSV będą się różnić od podanych poniżej w zależności od wykorzystanej funkcji konwertującej. W domyślne wartości w poniższych wzorach zakładają, że \(H \in <0,360)\), a \(S,V \in <0,100>\) co prawie na pewno nie będzie zgodne z waszymi przedziałami domyślnymi. Wartości te trzeba dostosować do waszych danych.

\[ H_{quant} (x , y)=\begin{cases} 0 & \text{ dla } H (x , y)<20 \text{ oraz } H ( x,y) \geq 316 \\ 1 & \text{ dla } 20 \leq H( x , y)<40 \\ 2 & \text{ dla } 40 \leq H (x , y )<75 \\ 3 & \text{ dla } 75 \leq H (x , y )<155 \\ 4 & \text{ dla } 155 \leq H (x , y)<190 \\ 5 & \text{ dla } 190 \leq H (x , y )<270 \\ 6 & \text{ dla } 270 \leq H (x , y)<295 \\ 7 & \text{ dla } 295 \leq H (x , y)<316 \end{cases} \]

\[ S_{quant} (x , y)=\begin{cases} 0 & \text{ dla } 0\leq S ( x , y)<20 \\ 1 & \text{ dla } 20\leq S (x , y )<70 \\ 2 & \text{ dla } 70\leq S ( x , y)\leq 100 \end{cases} \]

\[ V_{quant} (x , y)=\begin{cases} 0 & \text{ dla } 0\leq V ( x , y)<20 \\ 1 & \text{ dla } 20\leq V (x , y )<70 \\ 2 & \text{ dla } 70\leq V ( x , y)\leq 100 \end{cases} \]

Schematy w jaki sposób mniej więcej kwantyzują się kolory przedstawiono na obrazach poniżej.

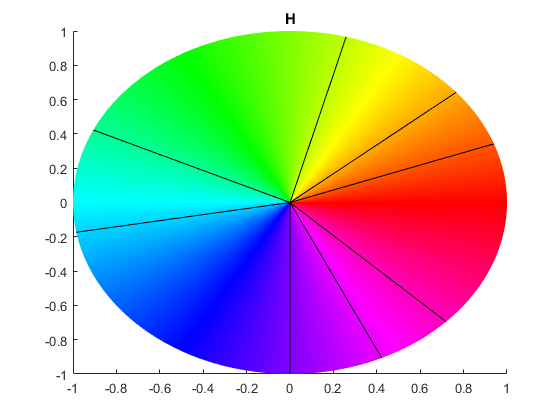
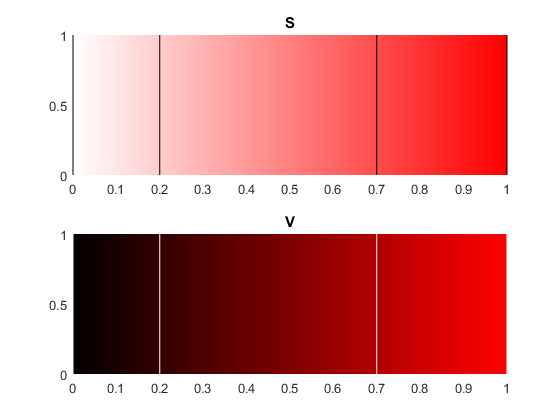
UWAGA Kolorów w przestrzeni HSV nie wyświetlamy na ekranie - jeżeli chcemy zaprezentować je na ekranie należy ponownie przenieść je do przestrzeni RGB.

Uproszczony algorytm EHD - Edge Histogram Descriptor

Uproszczony algorytm EHD wykorzystuje 80 przedziałów i jest realizowany w następujących krokach:

• Konwersja obrazu do odcieni szarości,
• Inicjalizacja histogramu H80 z 80 elementami,
• Podział obrazu na 16 bloków (4x4 bloki) - wielkość bloków może być różna dla różnych obrazów (mogą nie być kwadratowe),
• Dla każdego z 16 bloków budowa histogramu H5 z 5 elementami,
• Podział każdego bloku B na bloki S o rozmiarach 2x2 piksele (jeśli rozmiar na to nie pozwala, to w ostatnim wierszu lub kolumnie dodać zera!),
• Obliczenie splotu ¹ każdego bloku S z maskami kierunkowymi pokazanymi na wykładzie (5 wartości wynikowych!): Histogram sprawdza krawędzie pod kątami 90° \(\begin{bmatrix}1 & -1 \\ 1 & -1\end{bmatrix}\),0° \(\begin{bmatrix}1 & 1 \\ -1 & -1\end{bmatrix}\), 45° \(\begin{bmatrix}\sqrt{2} & 0 \\ 0 & -\sqrt{2}\end{bmatrix}\), 135° \(\begin{bmatrix}0 & \sqrt{2} \\ -\sqrt{2} & 0 \end{bmatrix}\) i bez określonego kierunku \(\begin{bmatrix}2 & -2 \\ -2 & 2 \end{bmatrix}\),
• Znalezienie maksymalnej odpowiedzi (bezwzględnej) i dla odpowiedniego kierunku zwiększenie indeksu w histogramie,
• Konkatenacja wszystkich 5-cio elementowych histogramów H5 w histogram H80,
• Normalizacja histogramu H80 poprzez podzielenie wartości przez ich sumę całkowitą,

Do realizacji splotu można wykorzystać funkcję filter2D z OpenCV.