Częstotliwość próbkowania

Częstotliwością próbkowania jest wartością określającą ilość próbek sygnału przypadającą na dany okres (domyślnie jest to sekunda). Częstotliwość próbkowania wpływa na możliwość odtworzenia dźwięków, ponieważ częstotliwość Nyquista będzie zawsze wynosiła jego połowę. Będzie to również obserwowane w widmie. Najczęściej stosowaną przy plikach audio (wave , mp3) częstotliwością próbkowania jest częstotliwość 44.1 kHz, czasami nazywana standardem CD. Jest ona powiązana z możliwością rejestracji dźwięków przez ludzkie ucho, które rejestruje dźwięki w zakresie od 20 Hz do około 20 kHz. Drugą najczęściej spotykaną częstotliwością jest 48 kHz nazywana standardem DVD, ona również pozwala odtworzyć pełen zakres słyszany przez ludzkie ucho. Większość studiów nagraniowych stosuje rejestrację w częstotliwościach będących wielokrotnościami 48 kHz (96, 192 kHz), ponieważ pozwalają one w płynny sposób przechodzić pomiędzy nimi bez użycia skomplikowanych technik resampling.

Rozdzielczość bitowa

Rozdzielczość bitowa określa dokładność, z jaką zapisana jest jedna próbka danych, określając ilość dostępnych dla niej bitów. Najpopularniejsze aktualnie formaty danych dźwiękowych opierają się na 16- lub 24- bitowych próbkach. Rzadziej spotykane są formaty 8- lub 32- bitowe. Na zajęciach będzie się zdarzać, że będziemy pracować i prowadzić badania na sztucznie tworzonych formatach o mniejszej ilości bitów, która nie będzie obsługiwana domyślnie przez biblioteki, a to będzie wymagało pewnych dodatkowych operacji.

Rozdzielczość bitowa określa zakres wartości, jakie mogą wystąpić we wczytywanym pliku. Owszem można wymusić zawsze jednolity tryb wczytywania danych (np. dtype=np.float32), ale nie zmienia to, z jaką dokładnością zapisane są dane oraz z jakim domyślnym typem są one wczytane. Domyślnie dla poszczególnych formatów dane wczytane powinny być w poniższych typach:

• 8-bitowe - typ uint8 - Uwaga! Wartość neutralna sygnału w tym przypadku oscyluje w okolicach 128 nie 0
• 16-bitowe - typ int16
• 24-bitowe i 32-bitowe - typ int32 lub float32

Jeżeli w jakimś przypadku macie problem z odtworzeniem lub zapisaniem dźwięku, bo przykładowo słychać tylko szumy, to prawdopodobnie jest problem z interpretacją typu i trzeba wymusić inny typ danych na zmiennej .astype().

Widmo

Widmo to rozkład natężenia różnych częstotliwości składowych dźwięku, jakie składają się na sygnał dźwiękowy. Pozwalają ona również zaobserwować, w jaki sposób niektóre modyfikacje sygnału wpływają na niego. Do wyznaczenia widma wykorzystujemy transformatę Fouriera. Informacje na temat tego, jak ona działa powinna być już przedstawiona w toku studiów, jeżeli jednak nie macie takiej wiedzy lub chcecie trochę poszerzyć wiedzę kilka informacji uzupełniających, to można dowiedzieć się tutaj:

1. Jak działa transformata Fouriera [ENG YT]
2. Fourier Series Animation using Circles

Wiedza ta nie jest niezbędna do zrozumienia tej instrukcji, ale może posłużyć do rozwiania wątpliwości. Powinniście wiedzieć, że analiza Fourierowska jest skuteczna tylko w przypadku, gdy analizowany sygnał jest niezmienny w czasie. Można to osiągnąć na sygnałach niezmiennych w czasie. Da się również badać sygnały zmienne w czasie przy zastosowaniu odpowiednich procedur dzielenia sygnału na okna, ale nie jest to częścią dzisiejszych zajęć, więc będziemy badać widmo tylko specjalnie przygotowanych sygnałów.

Kilka przykładów o sposobie wyświetlania widma. Wszystkie z nich wykorzystują te same biblioteki oraz działają na tym samym pliku dźwiękowym zawierającym 1 sekundę sinusa 440 Hz. Dla osób, które nie miały z tym styczności, polecam wyświetlić sobie poniższe wykresy i przybliżać rejon wierzchołka znajdującego się w okolicy 440 Hz, jak również pozmieniać sobie rozmiar widma, o którym mowa w dalszej części wprowadzenia i zobaczyć, jaki ma ono wpływ na widmo.

import numpy as np
import matplotlib.pyplot as plt
import scipy.fftpack
import sounddevice as sd
import soundfile as sf

data, fs = sf.read('sin440Hz.wav', dtype=np.int32)

Na początek najprostszy sposób wyświetlania widma, czyli wyświetleni modułu widma bez żadnych parametrów i modyfikacji. Osie w obu wykresach osie OX zostały zasilone odpowiednimi parametrami. W pierwszym wykresie jest to czas, w drugim natomiast są to częstotliwości.

plt.figure()
plt.subplot(2,1,1)
plt.plot(np.arange(0,data.shape[0])/fs,data)

plt.subplot(2,1,2)
yf = scipy.fftpack.fft(data)
plt.plot(np.arange(0,fs,1.0*fs/(yf.size)),np.abs(yf))
plt.show()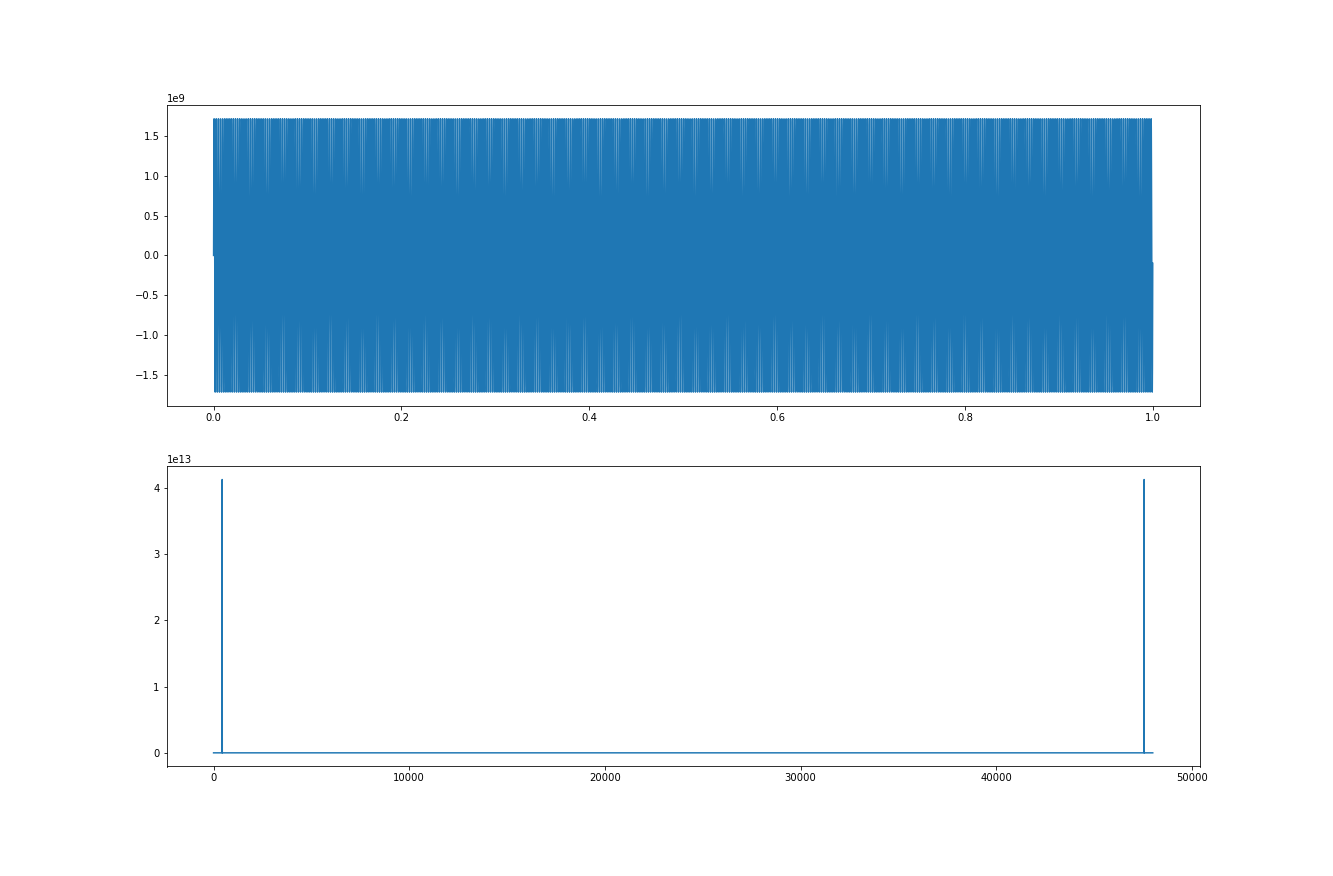

Kolejny przykład to moduł widma, ale w tym przypadku zmieniliśmy rozmiar transformaty Fouriera (w przykładzie do \(2^8=256\)), domyślny rozmiar jest zależny od długości sygnału. W przypadku Szybkiej Transformaty Fouriera, żeby odtworzyć w pełni sygnał, powinien być on pierwszą potęgą liczby \(2\), większą od długości naszego sygnału. W przypadku analizy naszego sygnału możemy go zmniejszyć, aby otrzymać mniej dokładane wyniki, ale w mniejszym nakładem czasu obliczeniowego oraz pamięci. Poniżej przykład, w którym zmniejszyliśmy rozmiar transformaty do 256. Oś OX w wykresie modułu widma została poprawiona, aby uwzględniać zmieniony jego rozmiar.

fsize=2**8

plt.figure()
plt.subplot(2,1,1)
plt.plot(np.arange(0,data.shape[0])/fs,data)

plt.subplot(2,1,2)
yf = scipy.fftpack.fft(data,fsize)
plt.plot(np.arange(0,fs,fs/fsize),np.abs(yf))
plt.show()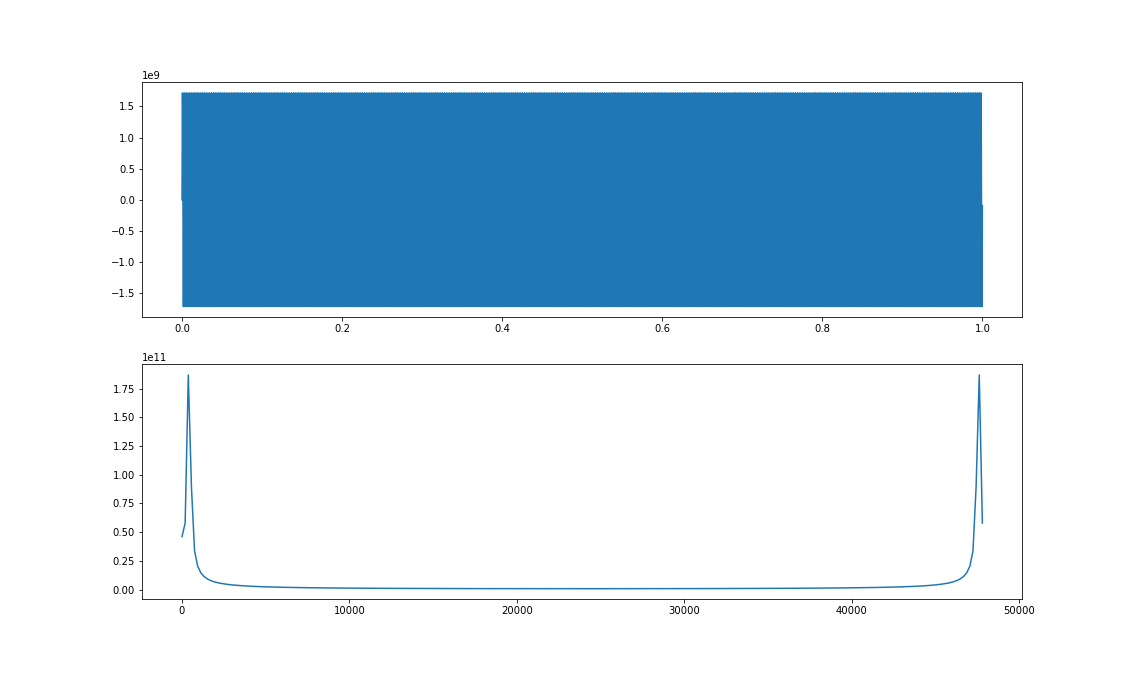

Kolejny etap wyświetlania modułu widma to wzięcie tylko połowy. Moduł widma jest symetryczny względem częstotliwości 0 Hz, więc przy jego wyświetlaniu możemy pominąć jedną z jego części:

plt.figure()
plt.subplot(2,1,1)
plt.plot(np.arange(0,data.shape[0])/fs,data)
plt.subplot(2,1,2)
yf = scipy.fftpack.fft(data,fsize)
plt.plot(np.arange(0,fs/2,fs/fsize),np.abs(yf[:fsize//2]))
plt.show()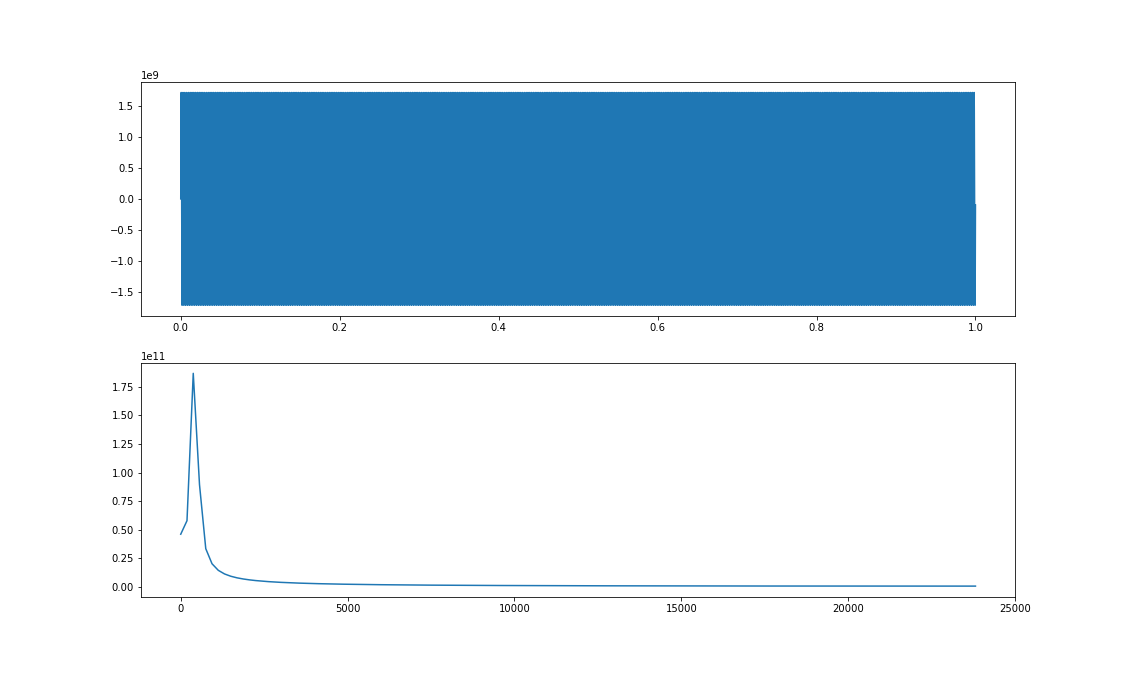

Ostatnią modyfikacją, którą możemy wykonać na naszym widmie w celu ułatwienia jego wyświetlania, jest jego przeskalowanie wartości widma do skali decybelowej (dB).

plt.figure()
plt.subplot(2,1,1)
plt.plot(np.arange(0,data.shape[0])/fs,data)
plt.subplot(2,1,2)
yf = scipy.fftpack.fft(data,fsize)
plt.plot(np.arange(0,fs/2,fs/fsize),20*np.log10( np.abs(yf[:fsize//2])))
plt.show()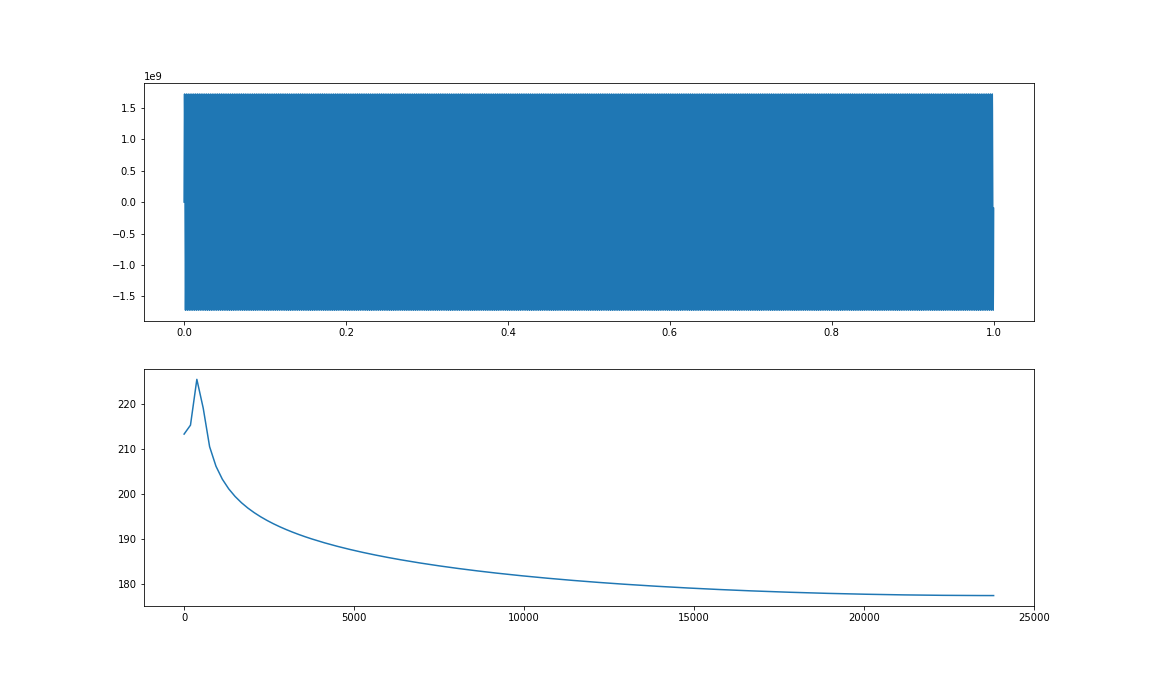

W powyższy sposób należy wyświetlać każde widmo, z jakim spotkacie się na zajęciach. Jedyny wyjątek będą stawiły niektóre szczególne przypadki, które będą dawały błędy dzielenia przez \(0\). W tych przypadkach warto wyświetlić widmo w skali liniowej i zastanowić się, czemu ten błąd wystąpił.