Materiał mający za zadanie przybliżyć podstawy dotyczące syntezy dźwięku. Uwaga: nie mam wykształcenia muzycznego, więc cześć z informacji może nie być całkowicie zgodna z teorią muzyki, jest ona raczej moim sposobem przybliżenia wam pewnych aspektów z jakimi możecie się spotkać w ramach pracy na waszą syntezą.

Generowanie fal dźwiękowych

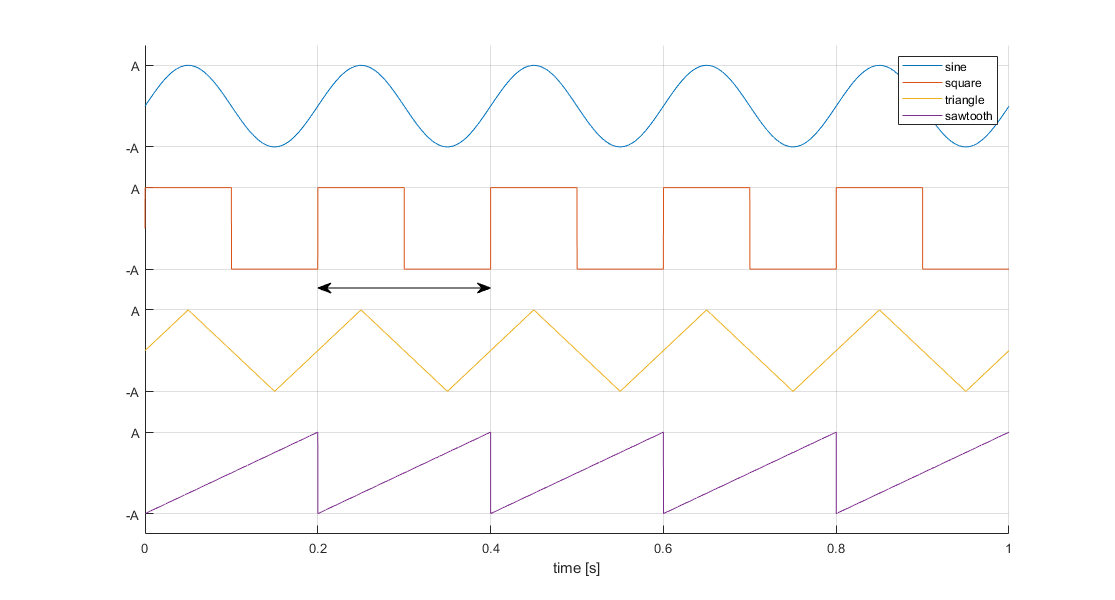
Żeby wygenerować dźwięk potrzebujemy kilku podstawowych informacji na temat sygnału, który chcemy wygenerować. Trzy najważniejsze to: typ fali dźwiękowej (lista poniżej), częstotliwość fali dźwiękowej (\(f\)) czyli ilość okresów funkcji jaka mieści się w 1 sekundzie sygnału oraz częstotliwość próbkowania sygnału (\(F_s\)) określająca z jakim kwantem czasu należy generować sygnał. Czas pomiędzy sąsiednimi próbkami (\(t(i)-t(i-1)\)) wynosi właśnie \(\dfrac{1}{F_s}\) sekund. Poniżej znajdują się zarówno wzory na poszczególne fale oraz wykresy dla nich (czarną strzałką został zaznaczony jeden okres funkcji). Faza sygnału (\(\varphi\)) określa o jaką część sygnału jesteśmy przesunięci w czasie, to znaczy jeżeli w jakimś oknie czasowym nie zmieścił się pełen okres sygnału to następne okno powinno zacząć się z odpowiednim przesunięciem fazowym w przeciwnym przypadku faza zawsze wynosi \(0\).

• Fala sinusoidalna: \(y(t)=A\sin(2\pi f t+\varphi)\)
• Fala prostokątna: \(y(t)=A \text{ sign}( \sin(2\pi f t+\varphi))\), gdzie \(\text{sign}(x)=\begin{cases}1\text{ ,wtedy gdy }x>0\\0\text{ ,wtedy gdy }x=0\\-1\text{ ,wtedy gdy }x<0\end{cases}\)
• Fala trójkątna: \(y(t)=\dfrac{2A}{\pi}\arcsin(\sin(2\pi f t+\varphi))\)
• Fala piło-kształtna: \(y(t)=-\dfrac{2A}{\pi}\arctan(\cot(\pi f t+\varphi))\)

Czym są nuty

Z wiadomości, które powinniście kojarzyć z edukacji wczesnoszkolnej powinniście pamiętać takie znaczki:

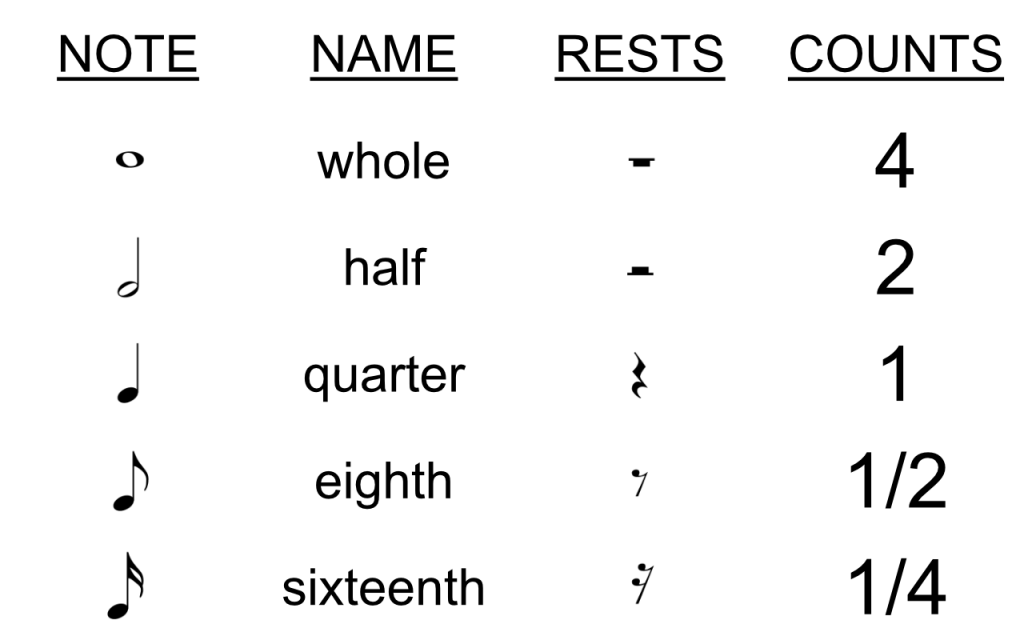
Są to nuty określają one jak długo ma trwać konkretny dźwięk. Powiązany jest z tym parametr zwany BPM czyli ‘Beats per Minute’, określa on ilość ćwierć-nut na minutę. Należy pamiętać o wzajemnych zależnościach pomiędzy nutami cała nuta (whole) trwa 4 razy dłużej niż ćwierć nuta, analogicznie półnuta (half) trwa dwa razy dłużej, ósemka (eighth) trwa połowę, a szesnastka (sixteenth) jedną czwartą.

Kolejna informacja, która może wam się przydać jest sugestia jak czytać klucze w zapisie nutowym klucz wiolinowy (pierwszy rząd) opisuje położenie dźwięku g w czwartej oktawie (\(g^1\)/g-razkreślne), natomiast klucz basowy (drugi rząd) opisuje położenie dźwięku f w trzeciej oktawie(\(f\)). Domyślne ich położenie pokazane jest na skrajnych lewych przykładach kluczy. Poniżej zaprezentowano przykład jak wyglądają nuty w ich relacji do poszczególnych kluczy oraz białych klawiszy fortepianu.

Częstotliwość podstawowa a nuta

Oczywiście oprócz samego symbolu określającego czas trwania dźwięku ważna jest jego wysokość. Wysokość dźwięku to wartość częstotliwości z jaką wibrują elementy instrumentu muzycznego np. struny w gitarze, powietrze w piszczałce lub struny głosowe u człowieka. Dźwięki te zapisywane są albo za pomocą umieszczenia symbolu nuty na odpowiedniej wysokości na pięciolinii lub za pomocą odpowiedniego zestawu znaków (Dźwięk). Związek tych zapisów z wysokością dźwięku można zobaczyć na poniższym rysunku:

Zaprezentowano na nim jedna oktawę dźwięku - odpowiada ona jednej gamie od C do C w następnej oktawie (znanej każdemu Polakowi jako solmizacyjne do, re, mi, fa, sol, la, si, do). Osiem w słowie oktawa odpowiada 8 białym klawiszom na fortepianie. Jednak w tym zakresie mamy aż 12 dźwięków oddalonym od siebie o pół tonu. Większość dźwięków oddalona od siebie jest o cały ton (np. C-D), ale niektóre są oddalone od siebie tylko o półtonu (np. E-F). W przypadku dźwięków oddalonych o cały ton występują dodatkowe półdźwięki opisywane za pomocą dodatkowych symboli (np. # jak C# - Cis). Te dźwięki odpowiadają czarnym klawiszom na fortepianie.

Te same dźwięki w dwóch sąsiednich oktawach są od siebie dwa razy większe lub mniejsze to znaczy dla częstotliwości \(200\) Hz dźwięk oktawę wyższy miałby częstotliwość \(2*200=400\) Hz, a dźwięk oktawę niższy \(200/2=100\) Hz. Poszczególne tony oddalone są od siebie o \(\sqrt[6]{2}\), a półtony oddalone są od siebie wzajemnie o \(\sqrt[12]{2}\). To znaczy że jeżeli mamy dźwięk o częstotliwości \(220\) Hz to dźwięk oddalony od 3 pełne tony będzie miał częstotliwość \(200*\sqrt[6]{2}*\sqrt[6]{2}*\sqrt[6]{2} = 282.8427\). Jak widać tego typu wyliczenia mogą być obarczone dość dużym błędem, dlatego do wyliczeń częstotliwości lepiej zastosować częstotliwość strojenia. W muzyce najczęściej stosuje się strojenie na A4 (a w 4 oktawie) po polsku nazywane a razkreślnym \(a^1\), któremu odpowiada częstotliwość \(F_t=440\) Hz. Wzór prezentuje się następująco:

\(f=2^{(O+\dfrac{n}{12})}F_t\), gdzie \(O\) to przesunięcie w ilości oktaw, a \(n\) to przesunięcie w górę lub w dół w ilości półtonów.

Warto przetestować czy wartości generowane dla was przez wasz program zgadzają się z wartościami jakie powinny zostać wygenerowane wartości na Wikipedii