Materiał mający za zadanie przybliżyć podstawy dotyczące syntezy dźwięku. Uwaga: nie mam wykształcenia muzycznego, więc cześć z informacji może nie być całkowicie zgodna z teorią muzyki, jest ona raczej moim sposobem przybliżenia wam pewnych aspektów z jakimi możecie się spotkać w ramach pracy na waszą syntezą.

Modulacja częstotliwości i amplitudy

W naszym syntezatorze możemy modulować dwa parametry: Częstotliwość, Amplitudę lub oba jednocześnie. W obu przypadkach potrzebujemy musimy posiadać amplitudę i częstotliwość zarówno dla funkcji modulującej jak i bazowej. W celu uproszczenia prezentacji we wszystkich przykładach wykorzystana jest funkcja sinus (\(\sin\)), ale powinna być możliwość zmiany na inną. Wszystkie przykłady modulacji oprócz wzorów matematycznych zostały zaprezentowane na wykresach.

Modulacja Amplitudy polega na przemnożeniu wartości naszej bazowej funkcji (\(B_f\)) poprzez wartości funkcji modulującej (\(A_m\)), należy jednak pamiętać że funkcja modulująca posiada zakres \(<-A,A>\), więc należy odpowiednio przesunąć jej wartości. Przykład na wykresie przedstawia modulację funkcji bazowej (\(f=40\) Hz, \(A=1\)) za pomocą funkcji modulującej (\(f=5\) Hz, \(A=0.25\)) przesuniętej w górę \(0.75\).

\[ B_f(t)=A_{base}\sin(2\pi f_{base} t+\varphi) \] \[ A_m(t)=A_{mod}\sin(2\pi f_{mod} t+\varphi) \] \[ y(t)=B_f(t)*A_m(t) \]

Modulacja Częstotliwości jest trochę bardziej skomplikowana opiera się w naszym przypadku na wzorze: \(\sin(2*\pi*\int f(t) \mathrm{d} t )\), który przekształca ciąg częstotliwości na przesunięcie fazowe funkcji. W przykładzie na wykresie mamy funkcję bazowa (\(f=40\) Hz, \(A=1\)) z funkcją modulująca częstotliwość (\(f=10\) Hz, \(A=10\)). We wzorze znajduje się kumulacyjna suma wszystkich poprzednich wartości, aż do bieżącej. To zadanie w realizuje dla nasz operacja np.cumsum.

\[ F_m(t)=f_{base} + A_{mod}\sin(2\pi f_{mod} t) \] \[ y(t)=A_{base}*\sin(2*\pi* \sum_{i=0}^{t}( \dfrac{F_m(i)}{Fs} )+\varphi) \]

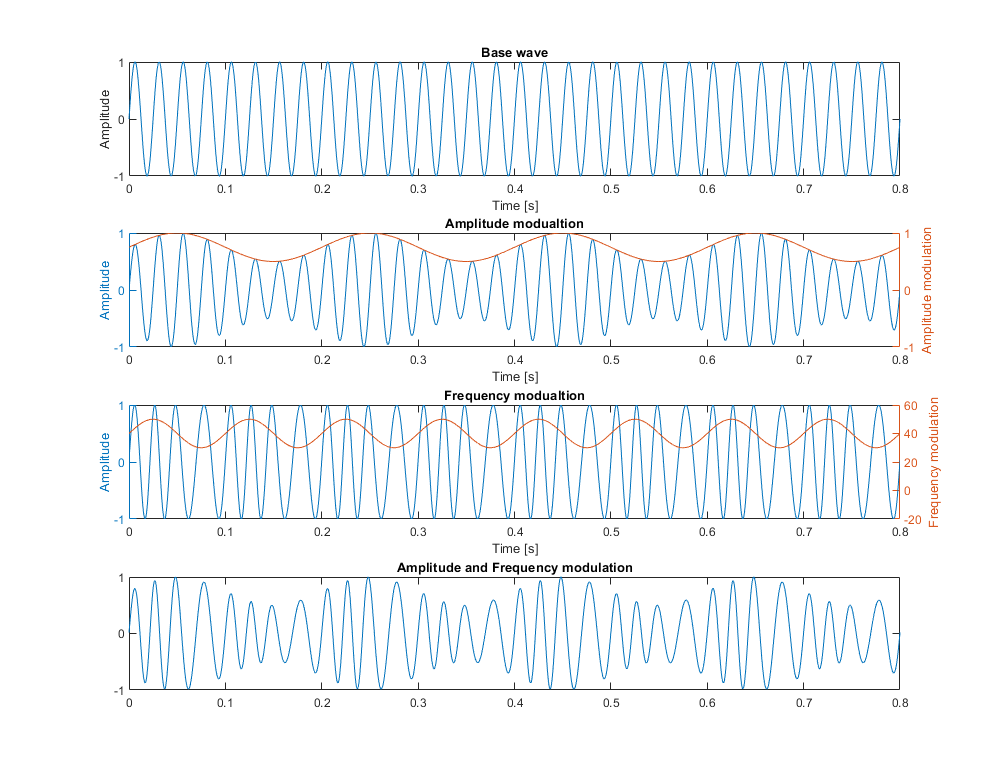
Modulacja częstotliwości i amplitudy wymaga połączenia obu powyższych metod. Przykład na wykresie pokazuje właśnie połączenie obu tych przykładów jednocześnie. Wpierw należy wykonać modulację częstotliwości, a następnie nanieść na nią modulację amplitudy.

Częstotliwości harmoniczne

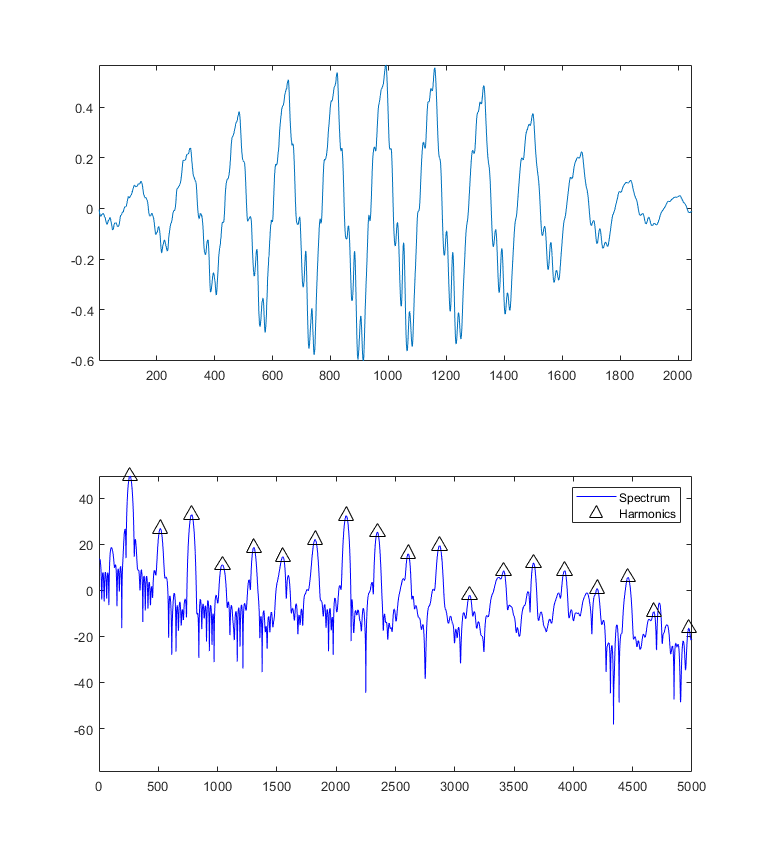
Budowany może zadanie symulować instrumenty harmoniczne, czyli takie w których występują ciągi harmoniczne częstotliwości. Ciąg taki zaczyna się od częstotliwości podstawowej (\(F_0\)) odpowiadającej wysokości dźwięku i każda kolejna częstotliwość ciągu jest wielokrotnością częstotliwości podstawowej (\(2*F_0\), \(3*F_0\), \(4*F_0\), itd.), różnią się one amplitudami. Na rysunkach poniżej przedstawiono poniżej. Pierwszy to zrzut z programu gdzie analizujemy widmo. Aby otrzymać widmo bierzemy fragment sygnału który analizujemy, następnie przemnażamy przez funkcję okna (np. okno Hamming) (górny wykres). Tak otrzymany fragment sygnału poddajemy działaniu Transformaty Fouriera. Widmo bez względu na ilość wartości jakie zawiera zakres częstotliwości \(<0,Fs>\) Hz lub \(<-Fs/2,Fs/2>\) w zależności od położenia jego centrum (wartość dla 0Hz). Wartości modułu widma (wartość bezwzględna) są symetryczne względem 0 Hz, więc interesuje nas tylko jego połowa \(<0,Fs/2>\) Hz. Otrzymane widmo przekształcamy na decybele (w drugiej części wykresu w wersji lekko powiększonej). Harmoniczne w naszym przypadku są wartościami wierzchołków o częstotliwościach zbliżonych do wielokrotności częstotliwości podstawowej, z przyczyn dokładności obliczeń wartości te mogą nie być dokładne i coraz bardziej odchylać się od wartości idealnej wraz ze wzrostem częstotliwości. Na wykresie zaznaczono kilka takich przykładowych harmonicznych.

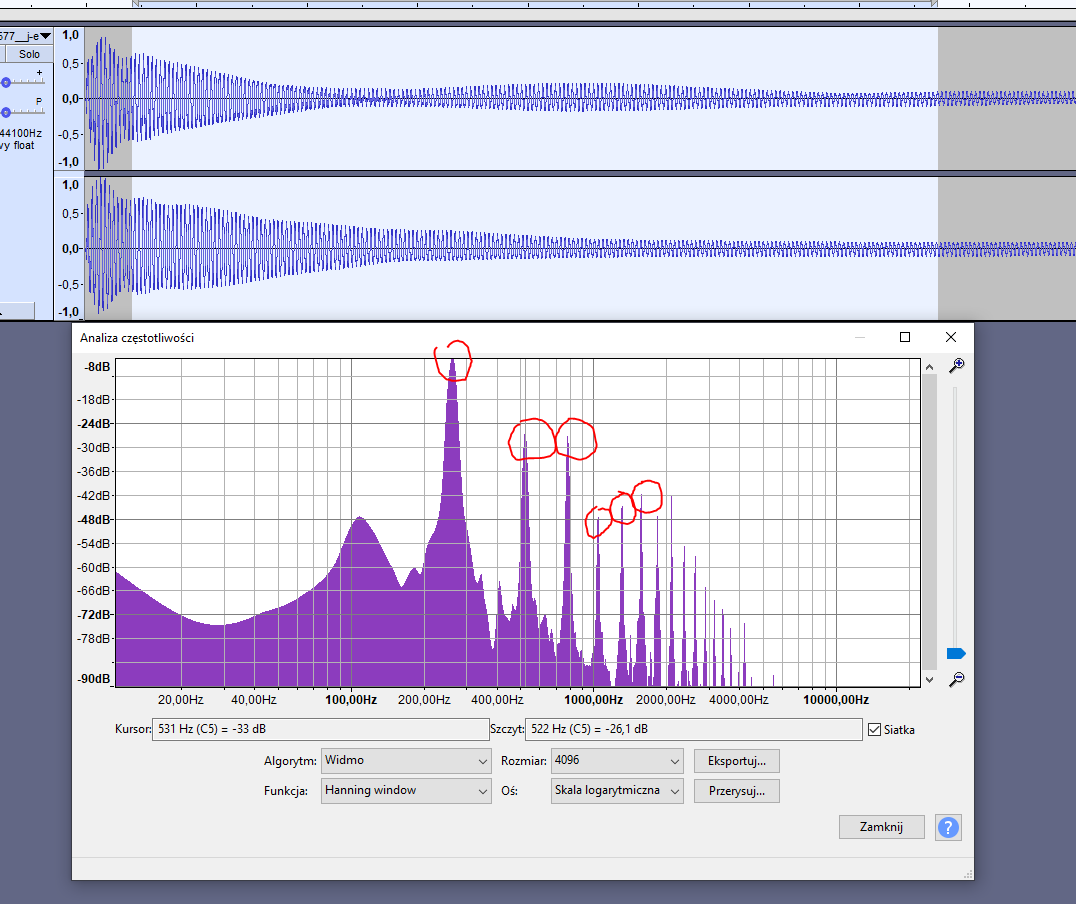
Drugi przykład lokalizacji harmonicznych przy wykorzystaniu programu Audacity. Czerwonymi okręgami zaznaczono potencjalne harmoniczne. Wartości ich częstotliwości oraz amplitud można odczytać z okienka opisanego jako Szczyt

W jaki sposób generujemy sygnał harmoniczny. Zakładając, że mamy dany wektor amplitud dla poszczególnych harmonicznych (w przypadku posiadania go w decybelach należy przekształcić go na wartości liniowe) możemy wykorzystać następujący wzór:

\[y(t)=A \sum_{i=1}^{N} \dfrac{A_iG(i*F_0,t)}{N}\]

(lub gdy amplitudy nowego sygnału będą wychodziły za wysokie)

\[y(t)=A \dfrac{\sum_{i=1}^{N}A_iG(i*F_0,t)}{\sum_{i=1}^{N}A_i}\]

Gdzie \(A\) to amplituda całkowita sygnału, \(A_i\) amplituda harmonicznej, \(G(f,t)\) - generator pojedynczej funkcji (np. sinusoidalnej), \(N\) liczba harmonicznych.