Podstawowym zadaniem naszej analizy danych opisanej w tym materiale to wyliczenie podstawowych statystyk na podstawie materiałów zbieranych podczas zajęć. Proszę nie traktować tego materiału jako wyczerpującego temat, a raczej jako podstawę przygotowania danych oraz zaproszenie do przejrzenia szeroko dostępnej literatury opisującej ten temat.
Dane
Na początku musimy przygotować nasze dane jako paczkę, którą można przystosować do obliczeń. Polecam wykorzystać w tym celu, różne listy, macierze NumPy lub pakiet Pandas, który jest wygodnym sposobem przechowywania danych wraz z nagłówkami i indeksami. Poniżej przykład jak stworzyć taką tablicę.
Base=pd.DataFrame(index=imges_names)
Base['Norms']=norms
Base['badany{u}_{r}'.format(u=user,r=rep)]=markDo danych możemy się odwoływać na kilka sposobów. Najwygodniejsze i najczęstsze są dwa:
- odwołanie się przez nagłówek
Base['Norms'] - za pomocą indeksów
Base.iloc[:,1:4]
Poniżej przykład sztucznie wygenerowanych danych, na jakich będziemy prezentować dalsze wyniki.
Norms_1 Norms_2 ... badany0_0 badany0_1 ... badany6_0 badany6_1 badany6_2
img0 98.306977 4.4982 ... 5.0 5.0 ... 5.0 5.0 5.0
img1 83.915634 6.0413 ... 3.0 5.0 ... 3.0 5.0 5.0
img2 73.294419 6.7655 ... 4.0 5.0 ... 4.0 5.0 5.0
img3 67.643601 7.5510 ... 4.0 5.0 ... 3.0 4.0 3.0
img4 56.500703 14.2819 ... 3.0 3.0 ... 4.0 3.0 4.0
img5 48.681885 15.4653 ... 2.0 3.0 ... 2.0 4.0 4.0
img6 42.601172 16.7210 ... 2.0 4.0 ... 4.0 4.0 3.0
img7 29.568651 21.9219 ... 1.0 1.0 ... 2.0 1.0 1.0
img8 17.138727 22.5428 ... 1.0 2.0 ... 2.0 2.0 2.0
img9 10.634845 22.4859 ... 2.0 1.0 ... 1.0 2.0 1.0Jeżeli nie chcecie go wykorzystywać, możecie przechowywać dane w dowolny sposób.
Przygotowywanie “par”
Do wyświetlania i/lub obliczania potrzebujemy odpowiednich wektorów danych. Najczęściej potrzebujemy 2-elementowych par danych (jakieś \(x\) i \(y\)). W przypadku prezentacji skali MOS jest to index obrazu, w pozostałych przypadkach są to wartości miar jakości. Gdy mamy pojedynczą kolumnę nie jest to problem, bo mamy prostą relację 1:1. Jeżeli jednak mamy ich więcej (3 podejścia dla jednego badanego, wszystkie pomiary dla wszystkich badanych itd.) to jest już znacznie trudniej, ponieważ musimy zwielokrotnić nasze dane (indeks obrazu/Miarę jakości) do odpowiedniej ilości zachowując przy tym odpowiednią relację powielanego elementu do jej oceny, zachowując przy tym odpowiednią strukturę danych — jedna kolumna na jeden parametr.
Najłatwiej to przetestować generując sobie zestawy sztucznych danych testowych i sprawdzić, czy wasza metoda odpowiednio łączy wam dane w zestawy. Przykładowo:
norms=np.arange(0,10)
user_id_rep=100*id+10*rep+np.arange(0,10)Pamiętajcie, że macie 3 stopnie uogólnienia dla wszystkich statystyk:
- Dla wszystkich par ocena miara jakości.
- Uśrednienie ocen w ramach ocen dla jednego badanego.
- Uśrednienie wszystkich ocen dla wszystkich badanych.
Warto napisać sobie funkcję, która przygotuje wam ten zestaw danych na podstawie dostarczonych przez was danych. Przykładowo możemy stworzyć funkcję przyjmującą za jeden parametr indeks obrazu/Miarę jakości, a jako drugi macierz z ocenami MOS. Na wyjściu będzie ona zwracać 3 macierze 2-kolumnowe:
- Każda ocena z drugiego parametru z przyporządkowaną wartością z pierwszego parametru.
- Każda średnia ocena dla użytkownika z przyporządkowaną wartością z pierwszego parametru.
- Pary średnia ocena dla wszystkich użytkowników z odpowiadającą im wartością z pierwszego parametru.
Propozycja funkcji:
def generatePairs(Norm,MOS):
####
return All, MeanPerPerson, MeanPerPicObliczanie statystyk — regresja liniowa
Do wyliczenia Regresji linowej potrzebujemy przygotowanych odpowiednich par danych stożonych na poprzednim etapie. Dla każdego ze stopni uogólnień oraz każdej miary jakości z osobna. Do obliczeń posłużymy się biblioteką sklearn:
from sklearn.linear_model import LinearRegressionNa samym początku tworzymy nasz model, a następnie uczymy go (metoda fit).
model = LinearRegression()
model.fit(x,y)Do wyciągnięcia odpowiednich danych służy nam metoda predict
pred_y=model.predict(np.array([x1,x2]).reshape(-1, 1))UWAGA Regresję linową liczymy tylko dla poszczególnych miar jakości nie dla indeksów obrazów !!!!!
Wyświetlanie
Wyświetlanie naszych ocen i relacji również wymaga przedstawienia mam 3 stopni uogólnienia. Jak widać na załączonych poniżej wizualizacjach. Podobnie jak w przypadku statystyk potrzebujemy, mieć tu pary odpowiadające punktom, jakie chcemy nanieść na wykresy. W celu uzyskania różnego rodzaju par symbol-kolor na wykresie można strwożyć tablicę zwierająca takie zestawy, a następnie podpiąć ją podczas wyświetlania, żeby wykorzystać jako odpowiedni odnośnik dla danego badanego.
symbol=['r*','g^','bv']
(...).plot( x, y ,symbol[i])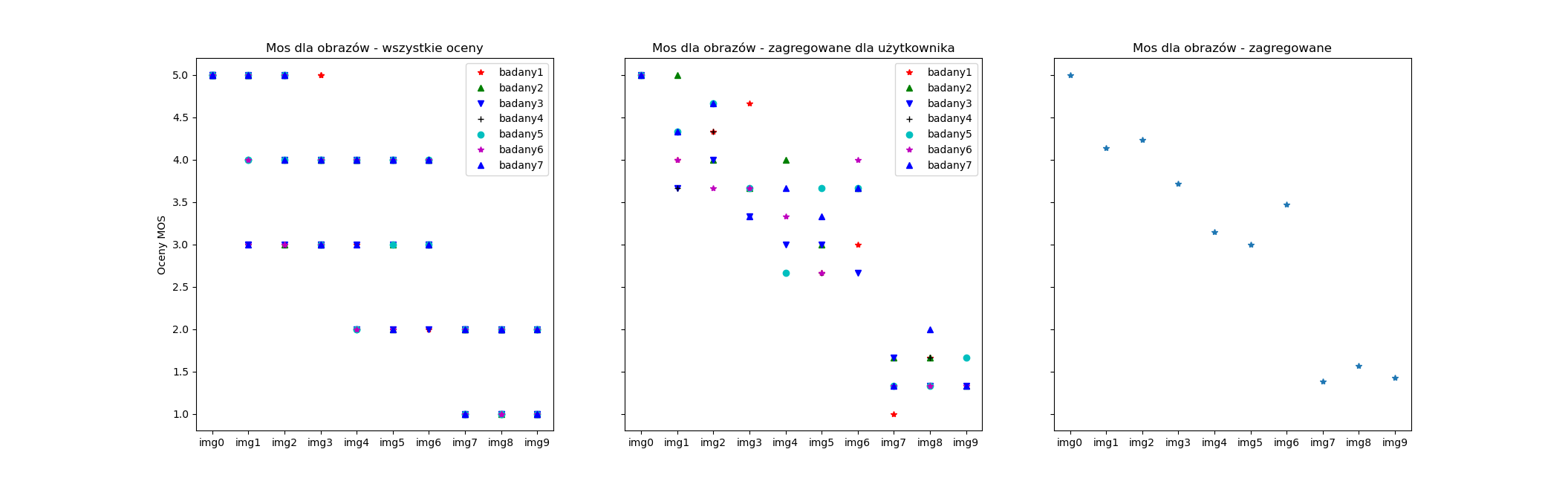
W celu naniesienia regresji liniowej najwygodniej jest ustalić jakiś punkt początkowy i końcowy (różny w zależności od naszych danych oraz wartości naszej miary jakości), a następnie sprawdzenie jaką wartość oczekiwaną zwracają dla nas w tym miejscu nasze modele. Na tej podstawie mamy dwie pary punktów (x1,y1_pred oraz x2,y2_pred) i możemy wyrysować za pomocą funkcji plot linię pomiędzy nimi (symbol -k).
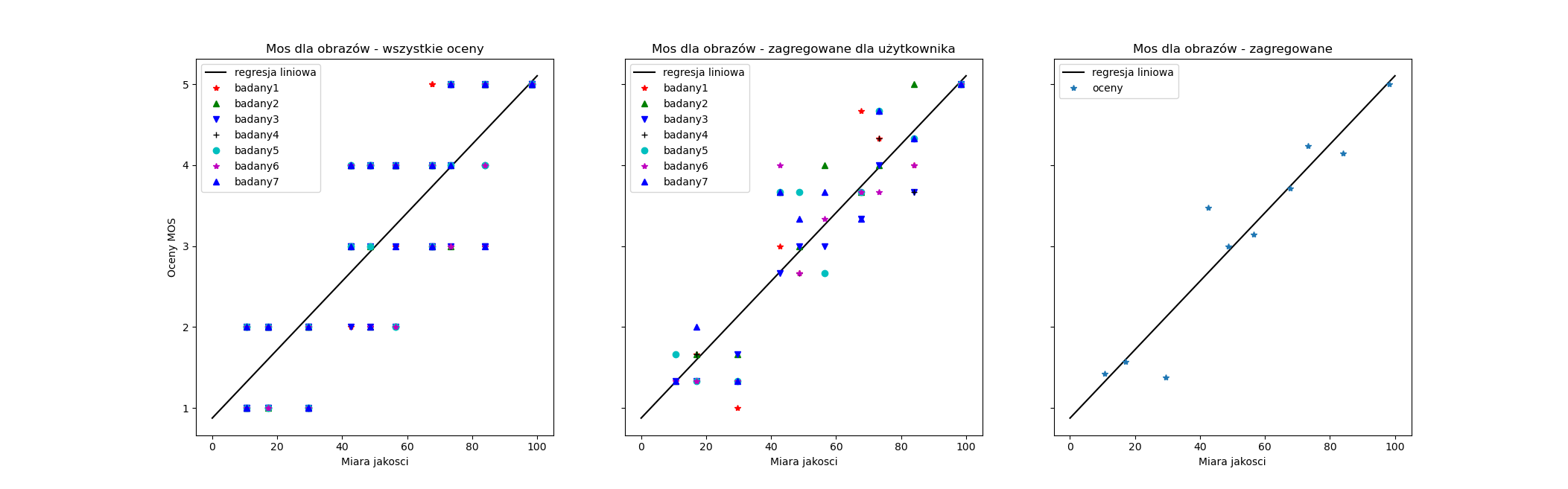
Obliczanie statystyk — Korelacja
Do obliczenia Korelacji będziemy wykorzystywać funkcje np.corrcoef. Podobnie jak w przypadku innych statystyk i wyświetlania przyjmuje ona dane w postaci macierzy, gdzie każdy wiersz opisuje ten sam element. W przeciwieństwie jednak do innych funkcji tu możemy na raz dokonać obliczeń na wielu “zestawach danych” jednocześnie. Czyli możemy przygotować sobie paczkę, gdzie w każdym z wierzy, będziemy mieli po kolei: MOS, Miarę jakości 1, Miarę jakości 2, itd. I dostaniemy na wyjściu nie tylko korelacje poszczególnych miar jakości w stosunku do MOS, ale również korelacje pomiędzy samymi miarami jakości względem waszych obrazów.
corr_matrix = np.corrcoef(xyz).round(decimals=2)Do wyświetlenia najlepiej wykorzystać mapy ciepła.
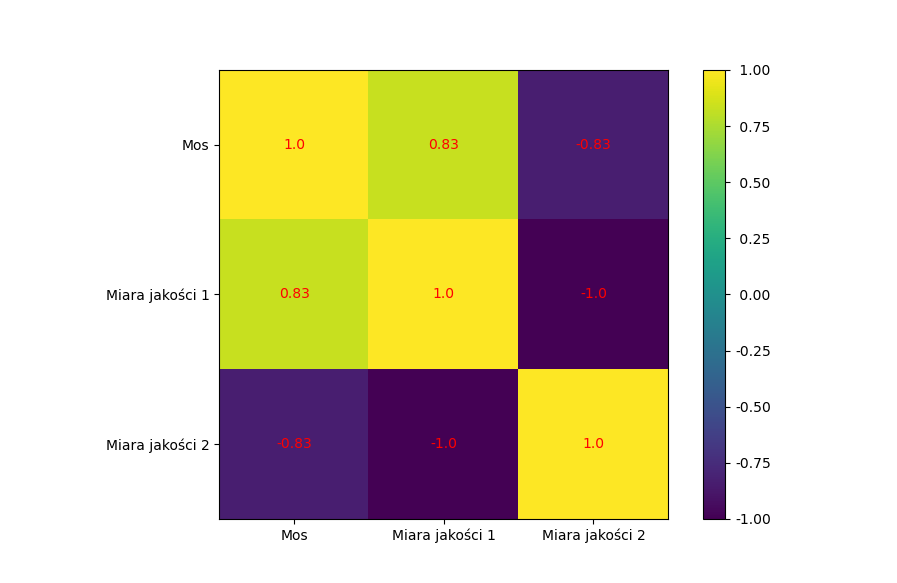
Ponieważ interesują nas głównie informacja o tym, jak bardzo powiązane są nasze miary jakości i wyniki są skorelowane, a nie czy jest to pozytywna, czy negatywna korelacja, możemy wyświetlić w naszej mapie ciepła wyświetlić wartości bezwzględne korelacji.