Algorytmy A-law i μ-law pracują na sygnałach float (\(<-1,1>\)). Praca z algorytmami law będzie przebiegała według schematu:

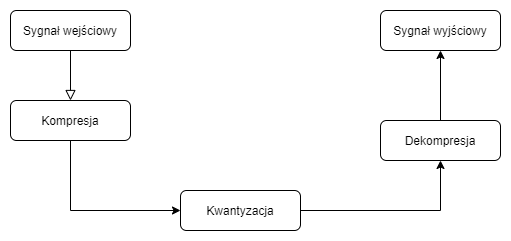
Algorytm A-law

Algorytm A-law jest standardem powszechnie stosowanym w 8-bitowej kompresji sygnału w Europie. Kompresja wykorzystuje zmniejszenie zakresu dynamicznego dla pewnych częstotliwości. Kompresja odbywa się za pomocą równania \(y=F(x)\), natomiast do dekompresji wykorzystujemy równanie \(x'=F^{-1}(y)\). W obu przypadkach wykorzystujemy parametr \(A=87.6\), który jest standardem. Sposób, w jaki wyglądają poszczególne krzywe kompresji oraz sygnał po dekompresji zaprezentowano pod koniec instrukcji.

\[ F(x) = {sign}(x) \begin{cases} \dfrac{A|x|}{1+\ln(A)}, & \quad \text{gdy } |x|<\dfrac{1}{A} \\ \\ \dfrac{1+ \ln(A |x|)}{1+\ln(A) }, & \quad \text{gdy } \dfrac{1}{A} \leq |x| \leq 1 \end{cases} \]

\[ F^{-1}(y) = {sign}(y) \begin{cases} \dfrac{|y|(1+\ln(A))}{A} , & \quad \text{gdy } |y|<\dfrac{1}{1+\ln(A)} \\ \\ \dfrac{\exp(|y|(1+\ln(A))-1)}{A} , & \quad \text{gdy } \dfrac{1}{1+\ln(A)} \leq |y| \leq 1 \end{cases} \]

Algorytm μ-law (lub mu-law)

Algorytm μ-law (mu-law lub u-law) jest standardem powszechnie stosowanym w 8-bitowej kompresji sygnału w stosowany w Stanach Zjednoczonych oraz Japonii. Kompresja wykorzystuje zmniejszenie zakresu dynamicznego dla pewnych częstotliwości. Kompresja odbywa się za pomocą równania \(y=F(x)\), natomiast do dekompresji wykorzystujemy równanie \(x'=F^{-1}(y)\). W obu przypadkach wykorzystujemy parametr \(\mu=255\), który jest standardem. Sposób, w jaki wyglądają poszczególne krzywe kompresji oraz sygnał po dekompresji zaprezentowano pod koniec instrukcji.

\[ F(x) = {sign}(x) \dfrac{\ln(1+\mu |x|)}{\ln(1+ \mu )}, \quad \text{gdy } -1 \leq x \leq 1 \]

\[ F^{-1}(y) = {sign}(y) \dfrac{1}{\mu}((1+\mu)^{|y|}-1), \quad \text{gdy } -1 \leq y \leq 1 \]

Funkcje, które potrzebujecie: funkcja znaku, logarytm naturalny, funkcja eksponencjalna:

np.sign()
np.log()
np.exp()

Uwagi końcowe i prezentacja działania

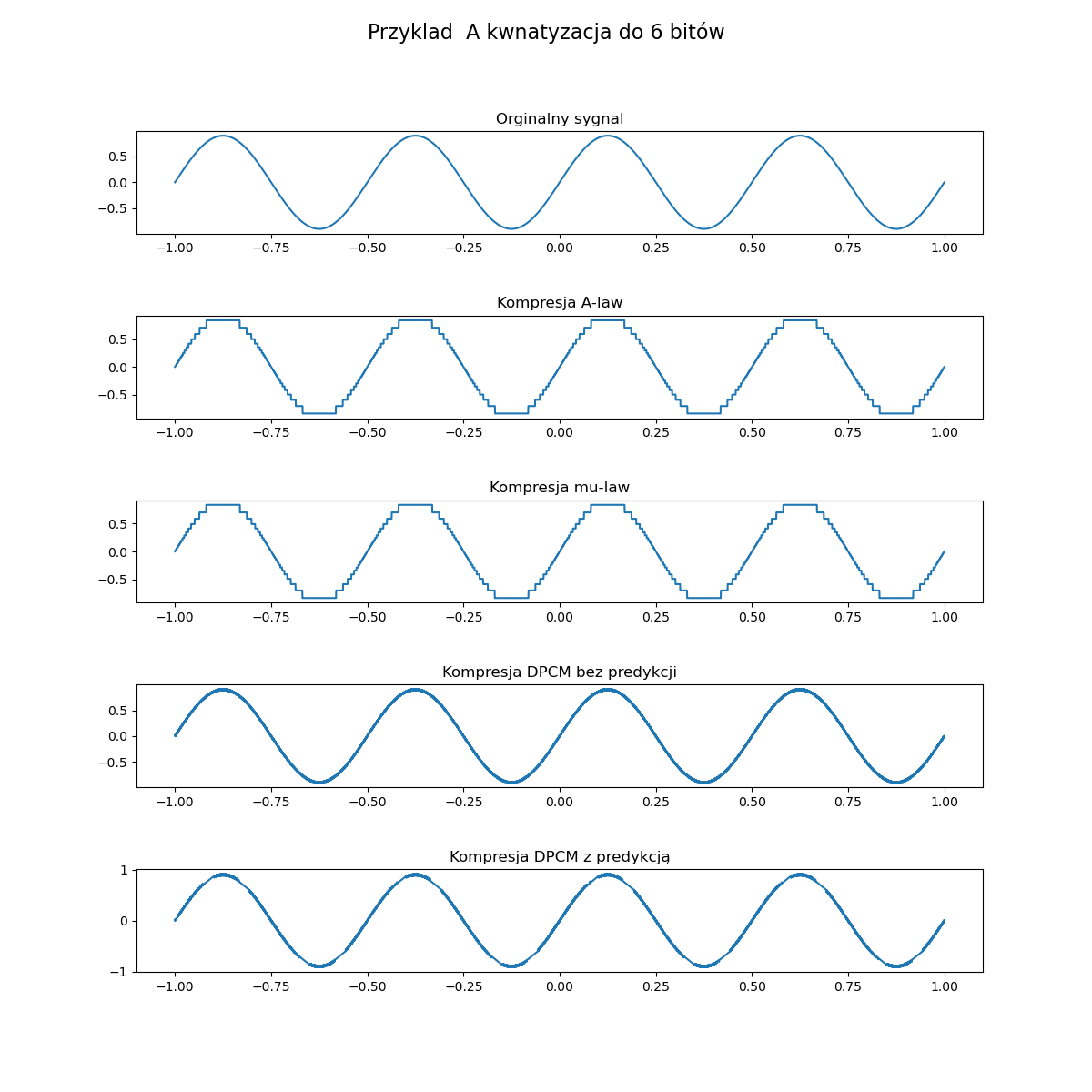
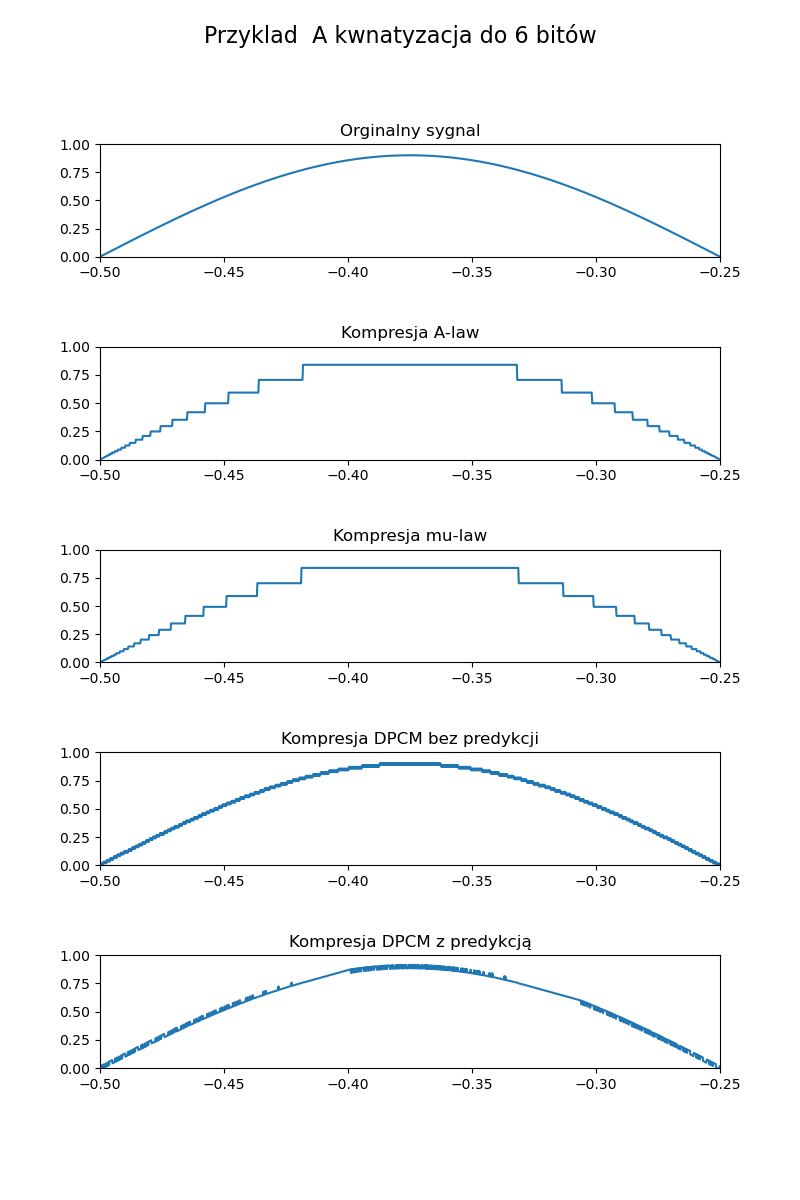
Wszystkie metody kompresji powinny działać po ich kwantyzacji do 8-bitów, chyba że jest popełniany jakiś błąd zaokrągleń. Jeżeli chodzi o testowanie prawidłowego działania metod law, to możemy je sprawdzić, wykorzystując tu aspekt, że kodują one całą przestrzeń sygnału. Na pełnej przestrzeni sygnału (np. x=np.linspace(-1,1,1000)) powinny się one prezentować jak na poniższych wykresach.

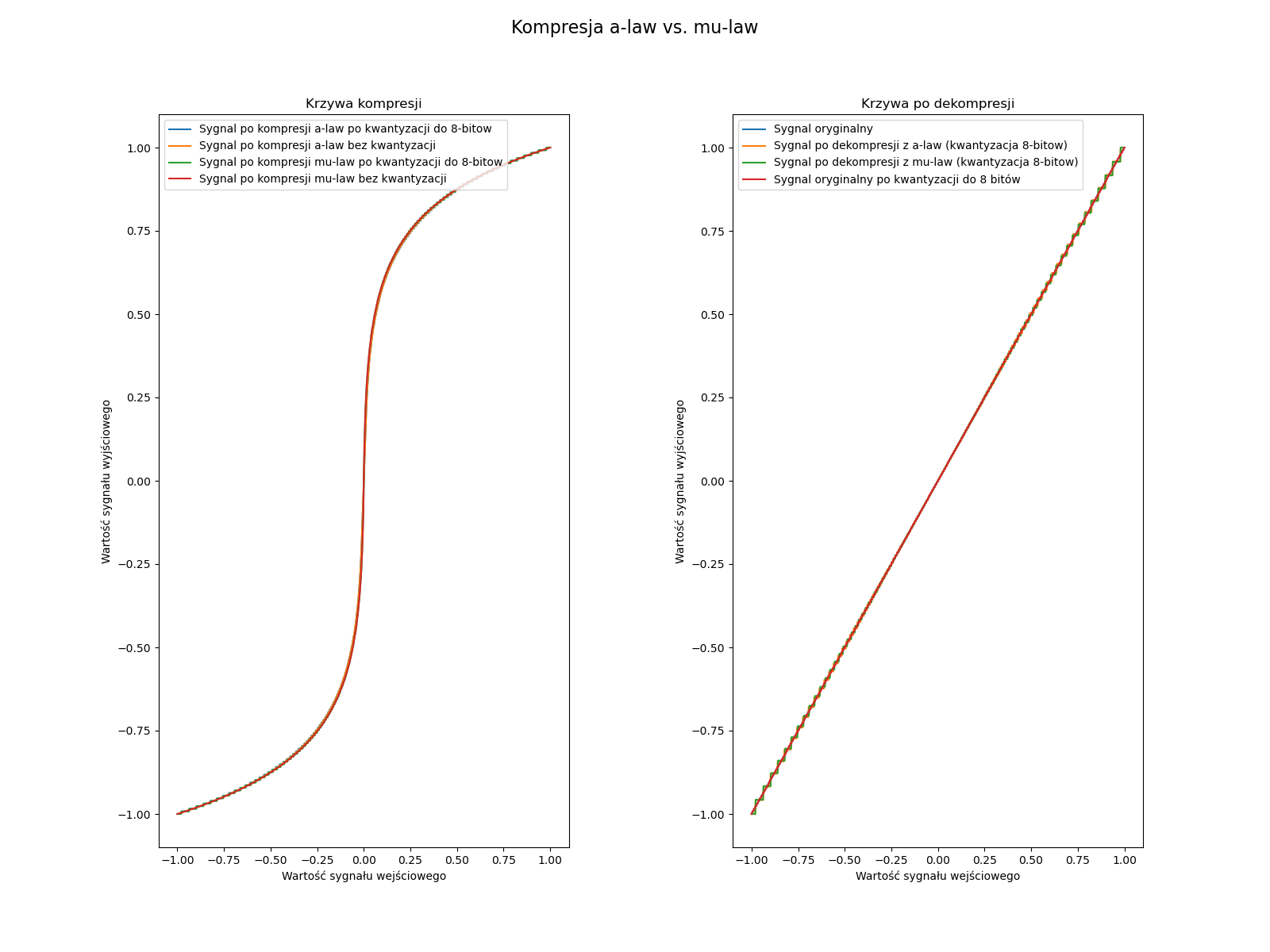
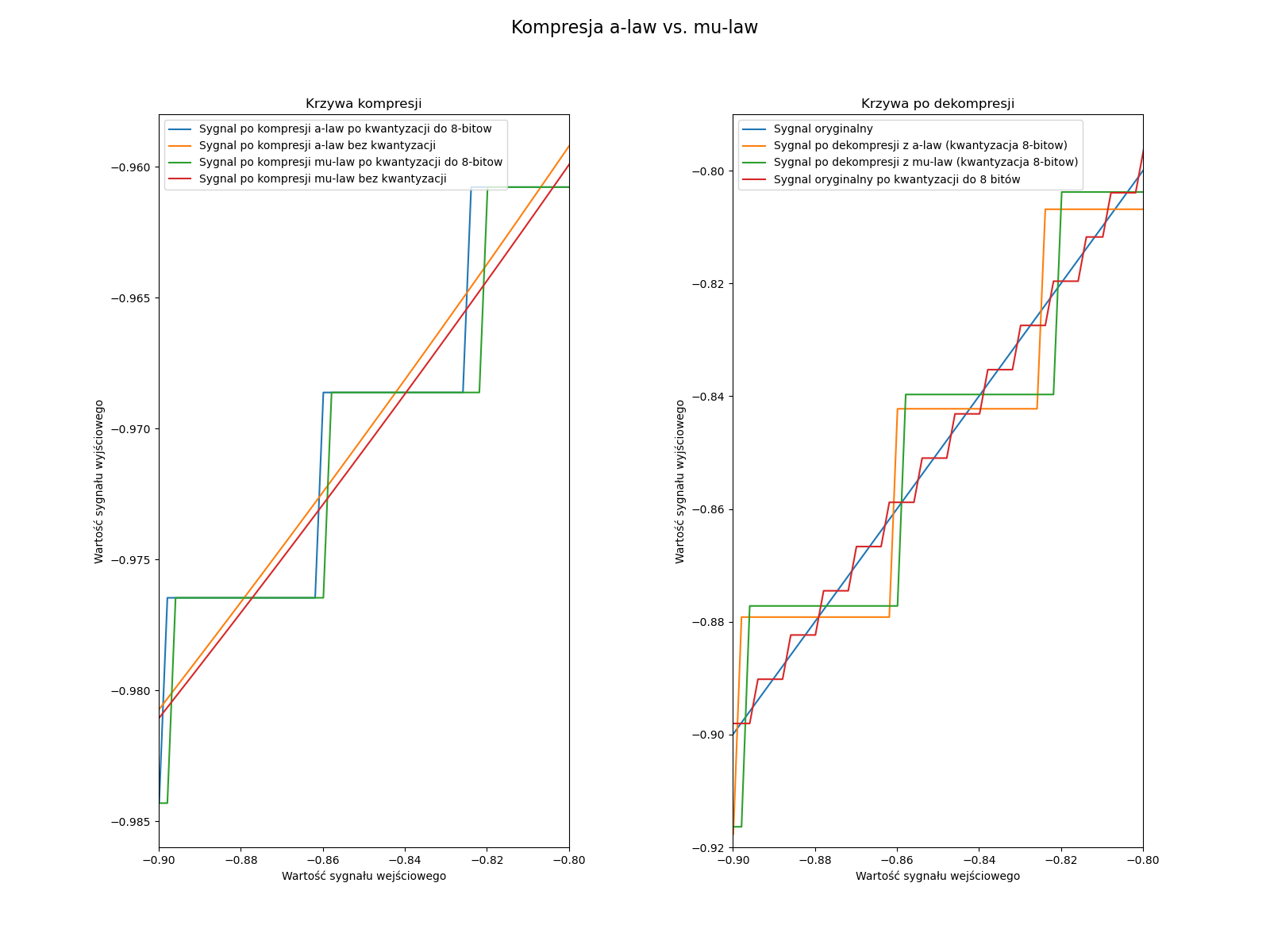
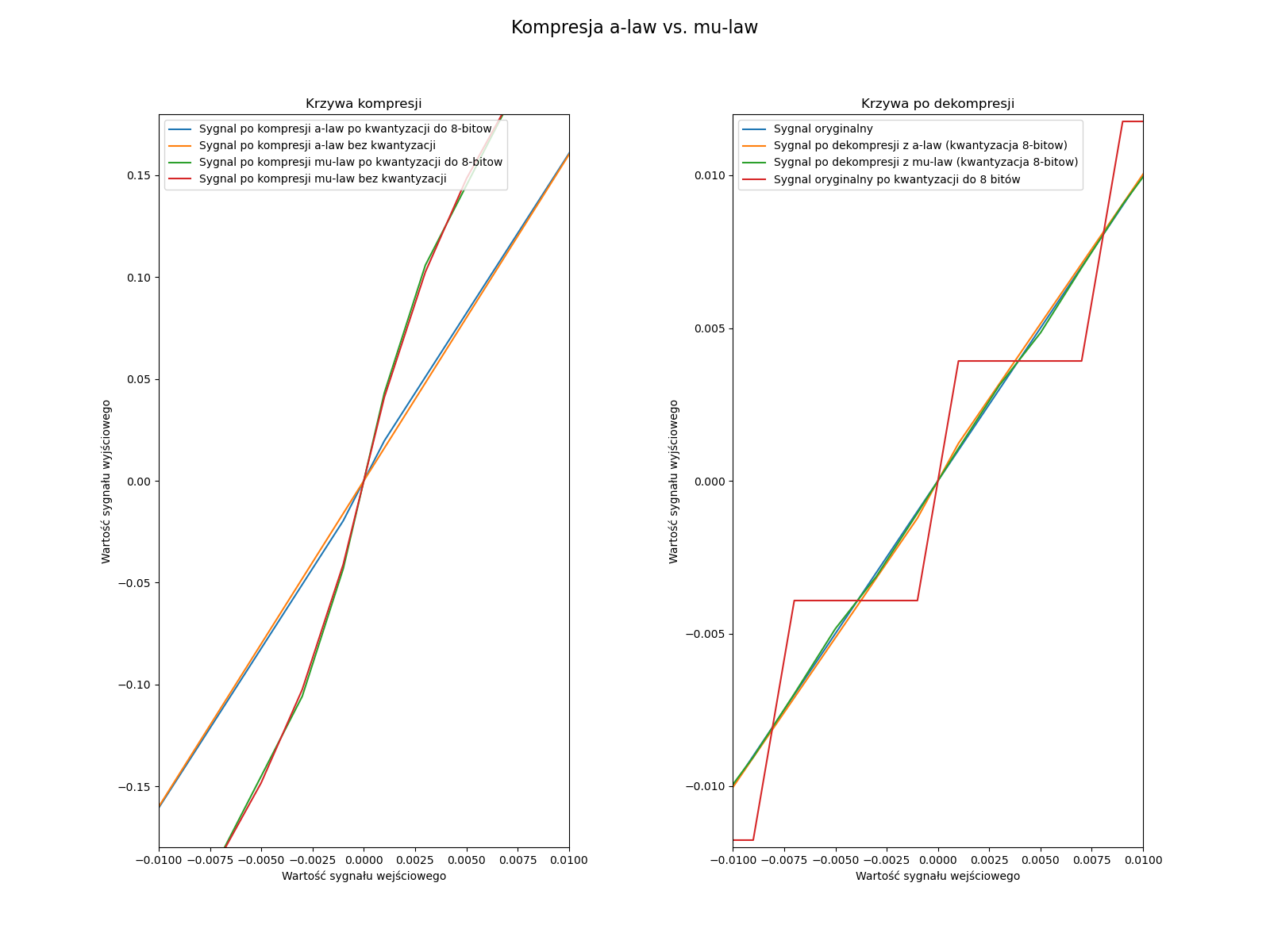
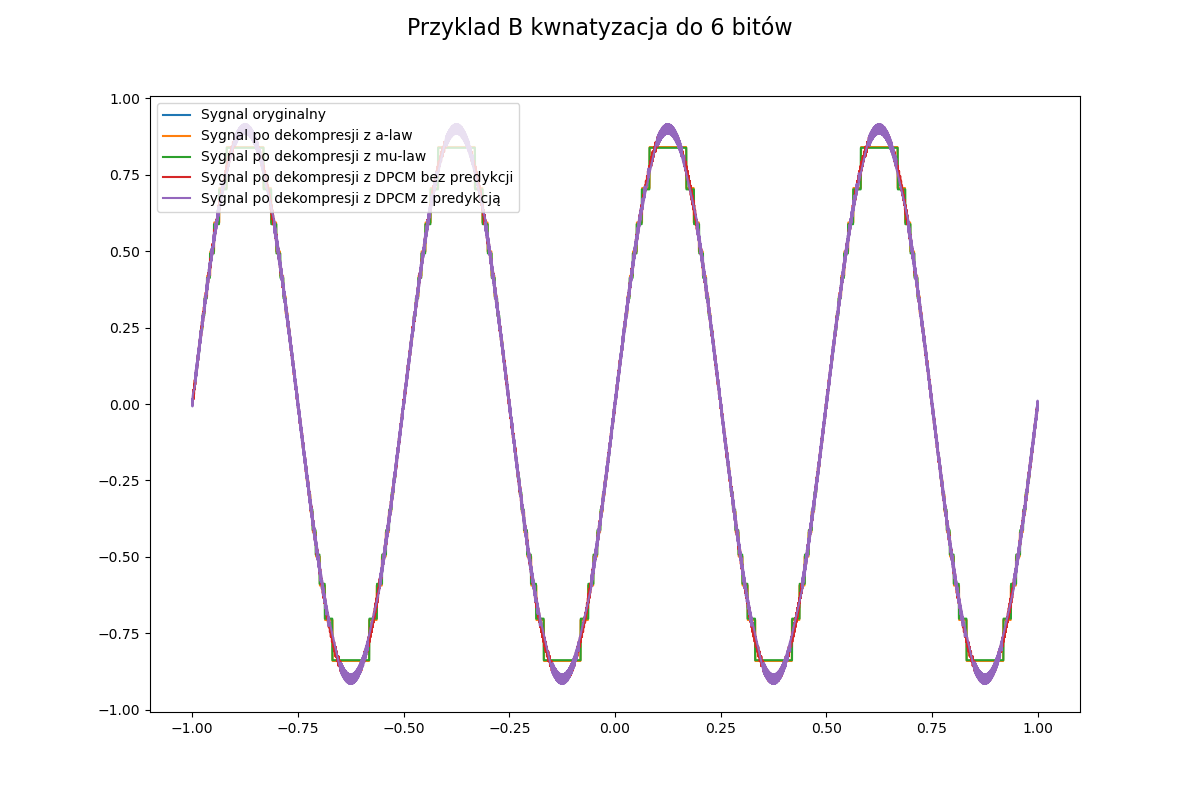
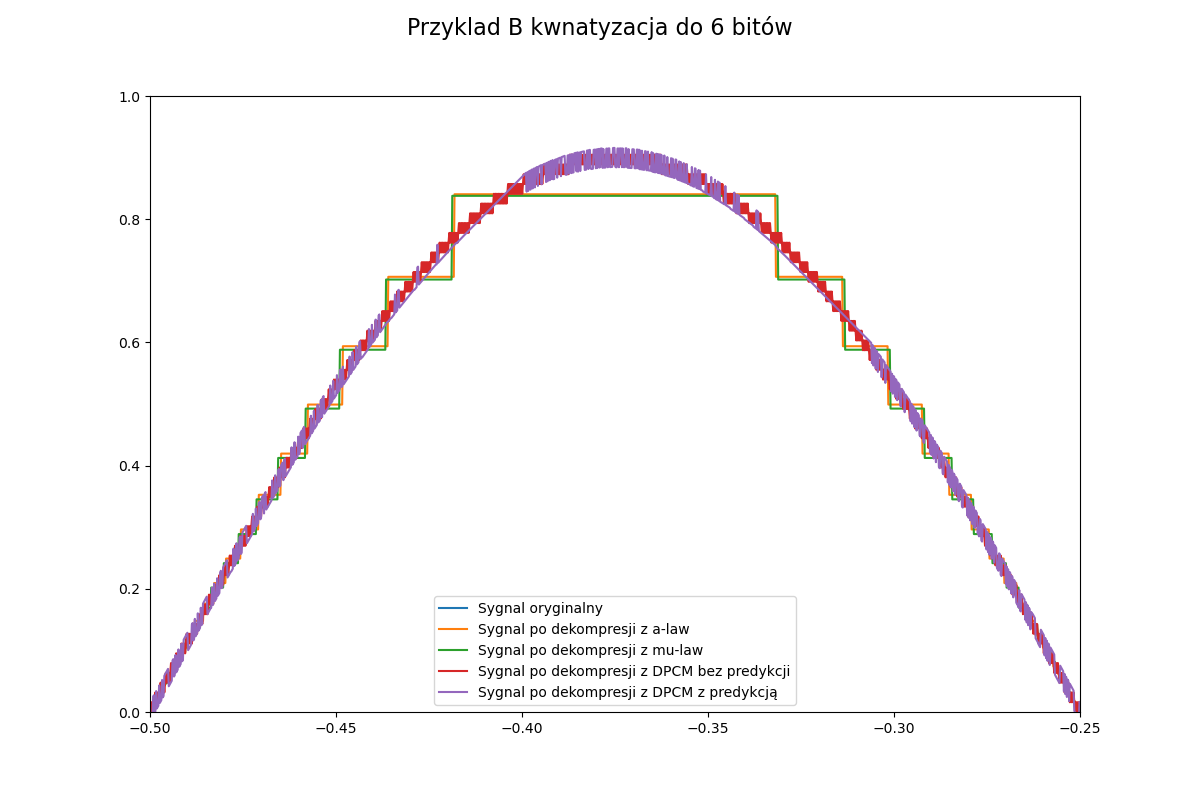
Jeżeli chodzi o porównanie wszystkich metod, to możemy zaobserwować na fragmencie sinusa (y=0.9*np.sin(np.pi*x*4) x z poprzedniego przykładu) jak poniżej. Możemy również za pomocą tego przykładu zobaczyć czy dobrze wykonujemy kompresję DPCM, gdy będzie coś nie tak, to będziemy widzieć obcinanie wartości lub inne dziwne spłaszczenia albo błędy.

Indeksowanie logiczne (jak łatwo zrobić A-law)

Indeksowanie logiczne to sposób, w jaki NumPy pozwala nam wykonywać operacje na części tabeli bez konieczności wykorzystywania pętli. Poniżej kilka linijek kodu, które pozwolą wam to zrozumieć. Uruchomcie sobie poniższe linijki w Pythonie i odpowiedzcie sobie pytanie, co dzieje się w zaznaczonych linijkach:

R=np.random.rand(5,5)
A=np.zeros(R.shape)
B=np.zeros(R.shape)
C=np.zeros(R.shape)


idx=R<0.25
A[idx]=1 # <-
B[idx]+=0.25 # <-
C[idx]=2*R[idx]-0.25 # <-
C[np.logical_not(idx)]=4*R[np.logical_not(idx)]-0.5 # <-
print(R)
print(A)
print(B)
print(C)