Pliki potrzebne do zadania:
Część pierwsza — dźwięk podstawowe informacje
Większość informacji na temat dźwięku powinniście znać z wcześniejszych przedmiotów (np. Transmisji Danych), jeżeli jednak nie pamiętacie, to dostaniecie tu krótkie przypomnienie najbardziej podstawowych informacji na ten temat.
Częstotliwość próbkowania
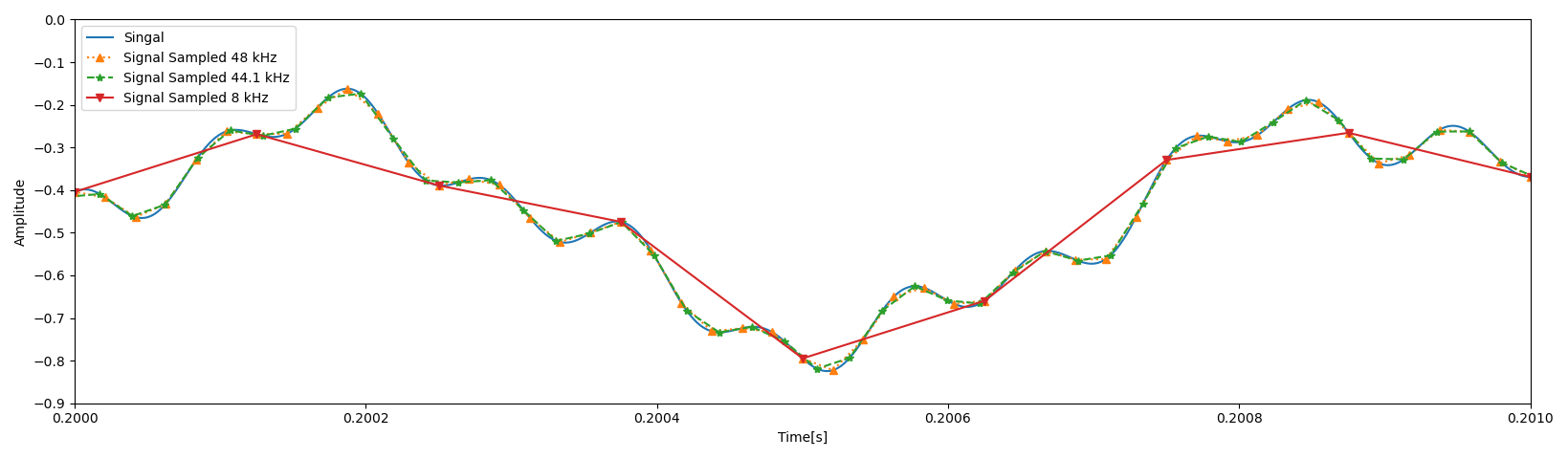
Częstotliwością próbkowania jest wartością określającą ilość próbek sygnału przypadającą na dany okres (domyślnie jest to sekunda). Częstotliwość próbkowania wpływa na możliwość odtworzenia dźwięków, ponieważ częstotliwość Nyquista będzie zawsze wynosiła jego połowę. Będzie to również obserwowane w widmie. Najczęściej stosowaną przy plikach audio (wave , mp3) częstotliwością próbkowania jest częstotliwość 44.1 kHz, czasami nazywana standardem CD. Jest ona powiązana z możliwością rejestracji dźwięków przez ludzkie ucho, które rejestruje dźwięki w zakresie od 20 Hz do około 20 kHz. Drugą najczęściej spotykaną częstotliwością jest 48 kHz nazywana standardem DVD, ona również pozwala odtworzyć pełen zakres słyszany przez ludzkie ucho. Większość studiów nagraniowych stosuje rejestrację w częstotliwościach będących wielokrotnościami 48 kHz (96, 192 kHz), ponieważ pozwalają one w płynny sposób przechodzić pomiędzy nimi bez użycia skomplikowanych technik resamplingu.
Rozdzielczość bitowa
Rozdzielczość bitowa określa, z jaką dokładność zapisana jest jedna próbka danych, podając ilość dostępnych dla niej bitów. Najpopularniejsze aktualnie formaty danych dźwiękowych opierają się na 16- lub 24- bitowych próbkach. Rzadziej spotykane są formaty 8- lub 32- bitowe. Na zajęciach będzie się zdarzać, że będziemy pracować i prowadzić badania na sztucznie tworzonych formatach o mniejszej ilości bitów, która nie będzie obsługiwana domyślnie przez biblioteki, a to będzie wymagało pewnych dodatkowych operacji.
Rozdzielczość bitowa określa zakres wartości, jakie mogą wystąpić we wczytywanym pliku. Owszem można wymusić zawsze jednolity tryb wczytywania danych (np. dtype=np.float32), ale nie zmienia to zawartości pliku, czyli tego, z jaką dokładnością oraz typem dane zostały zapisane. Domyślnie dla poszczególnych formatów dane wczytane powinny być w poniższych typach:
- 8-bitowe - typ
uint8- Uwaga! Wartość neutralna sygnału w tym przypadku oscyluje w okolicach128nie0 - 16-bitowe - typ
int16 - 24-bitowe i 32-bitowe - typ
int32lubfloat32
Jeżeli w jakimś przypadku macie problem z odtworzeniem lub zapisaniem dźwięku, bo przykładowo słychać tylko szumy, to prawdopodobnie jest problem z interpretacją typu i trzeba wymusić inny typ danych na zmiennej .astype().
Część druga — wczytywanie i zapisywanie plików dźwiękowych
Do tej części instrukcji, a zwłaszcza fragmentów wymagających odsłuchiwania polecam zakładać słuchawki, aby nie denerwować swojego otoczenia.
Do tego zadania dołączony jest jeden plik dźwiękowy w formacie wave. Zaczynamy od stworzenia nowego skryptu. Nazwijmy go np.: Lab_sound_1.py. Zacznijmy od zaimportowania odpowiednich bibliotek, w tym przypadku będą to:
import numpy as np
import matplotlib.pyplot as plt
import sounddevice as sd
import soundfile as sfZacznijmy od wczytania pliku dźwiękowego. Służy do tego komenda:
data, fs = sf.read('sound1.wav', dtype='float32') Dostajemy dwa zestawy danych pierwszy to tablica zawierająca wartości próbek sygnału, każda z jej kolumn zawiera osobny kanał wartości (domyślnie 2 to Lewy i Prawy). Jeżeli wywołamy komendy jak przypadku obrazu (zapisane poniżej), to zauważymy również że typ naszej tablicy będzie zgodny z typem podanym w parametrze wywołania funkcji wczytującej plik. Drugi parametr to częstotliwość próbkowania, czyli jak często sygnał rzeczywisty był próbkowany, czyli jak wiele próbek znajduje się w jednej sekundzie trwania dźwięku.
print(data.dtype)
print(data.shape)Teraz spróbujmy odtworzyć nasz dźwięk, wykorzystując zestaw komend:
sd.play(data, fs)
status = sd.wait()Pierwsza z nich odpowiada za rozpoczęcie odtwarzania. Druga zapewnia, że program poczeka z wykonaniem kolejnych instrukcji do momentu, aż dźwięk skończy się odtwarzać.
Zadanie Dźwięk 1
Zadanie polega na wczytaniu pliku sound1.wav i na jego podstawie wygenerowaniu trzech jedno-kanałowych plików wave (i sprawdzeniu ich poprawności albo za pomocą Pythona (wykorzystując część 3 zadania) albo jakiegoś programu do obróbki dźwięku czy zrobiono to poprawnie). Plik traktujemy jako tablice i w ten sposób wybieramy fragmenty, które nas interesują. Pliki powinny zawierać:
sound_L.wav- lewy kanał audio oryginalnego pliku,sound_R.wav- prawy kanał audio oryginalnego pliku,sound_mix.wav- jeden kanał mono będący średnimi wartościami poszczególnych próbek pochodzących z oryginalnego pliku audio (z obu głośników/słuchawek powinien wydobywać się ten sam dźwięk).
Do zapisu danych do pliku wave wykorzystujemy funkcję:
sf.write('nazwa.wav', new_data, fs)Część trzecia — wyświetlanie sygnału w czasie i widma dźwięku
Teraz spróbujmy wyświetlić nas sygnał na wykresie. Osobno dla każdego z kanałów. Przykładowo dla pierwszego z nich będzie to wyglądać:
plt.subplot(2,1,1)
plt.plot(data[:,0])Co możemy analogicznie zastosować do drugiego kanału. Mamy jednak problem na osi OX mamy w tym momencie tylko numery próbek a chcielibyśmy, żeby była ona w sekundach. Rozwiązać to można podając parametr x w plt.plot(x,data[:,0]).
Jak to zrobić wykorzystując do tego tylko:
- Dane wczytane z pliku (
dataifs), - Funkcję
np.arange, - Informacje podane już w instrukcji.
Widmo
Widmo to rozkład natężenia różnych częstotliwości składowych dźwięku, jakie składają się na sygnał dźwiękowy. Pozwalają ona również zaobserwować, w jaki sposób niektóre modyfikacje sygnału wpływają na niego. Do wyznaczenia widma wykorzystujemy transformatę Fouriera. Informacje na temat tego, jak ona działa powinna być już przedstawiona w toku studiów, jeżeli jednak nie macie takiej wiedzy lub chcecie trochę poszerzyć wiedzę o kilka informacji uzupełniających, to można dowiedzieć się tutaj:
- Jak działa transformata Fouriera [ENG YT]
- Fourier Series Animation using Circles
Wiedza ta nie jest niezbędna do zrozumienia tej instrukcji, ale może posłużyć do rozwiania wątpliwości. Powinniście wiedzieć, że analiza Fourierowska jest skuteczna tylko w przypadku, gdy analizowany sygnał jest niezmienny w czasie. Można to osiągnąć na sygnałach niezmiennych w czasie. Da się również badać sygnały zmienne w czasie przy zastosowaniu odpowiednich procedur dzielenia sygnału na okna, ale nie jest to częścią dzisiejszych zajęć, więc będziemy badać widmo tylko specjalnie przygotowanych sygnałów.
Kilka przykładów o sposobie wyświetlania widma. Wszystkie z nich wykorzystują te same biblioteki oraz działają na tym samym pliku dźwiękowym zawierającym 1 sekundę sinusa 440 Hz, plik ten dołączony jest materiałów i sugeruję testować na nim tę część zadania. Dla osób, które nie miały z tym styczności, polecam wyświetlić sobie poniższe wykresy i przybliżać okolicę wierzchołka znajdującego się w okolicy wartości 440 Hz na osi OX, jak również pozmieniać sobie rozmiar widma, o którym mowa w dalszej części wprowadzenia i zobaczyć, jaki ma ono wpływ na widmo i wierzchołek.
import numpy as np
import matplotlib.pyplot as plt
import scipy.fftpack
import sounddevice as sd
import soundfile as sf
data, fs = sf.read('sin440Hz.wav', dtype=np.int32)Na początek najprostszy sposób wyświetlania widma, czyli wyświetleni modułu widma bez żadnych parametrów i modyfikacji. Osie w obu wykresach osie OX zostały zasilone odpowiednimi parametrami. W pierwszym wykresie jest to czas, w drugim natomiast są to częstotliwości.
plt.figure()
plt.subplot(2,1,1)
plt.plot(np.arange(0,data.shape[0])/fs,data)
plt.subplot(2,1,2)
yf = scipy.fftpack.fft(data)
plt.plot(np.arange(0,fs,1.0*fs/(yf.size)),np.abs(yf))
plt.show()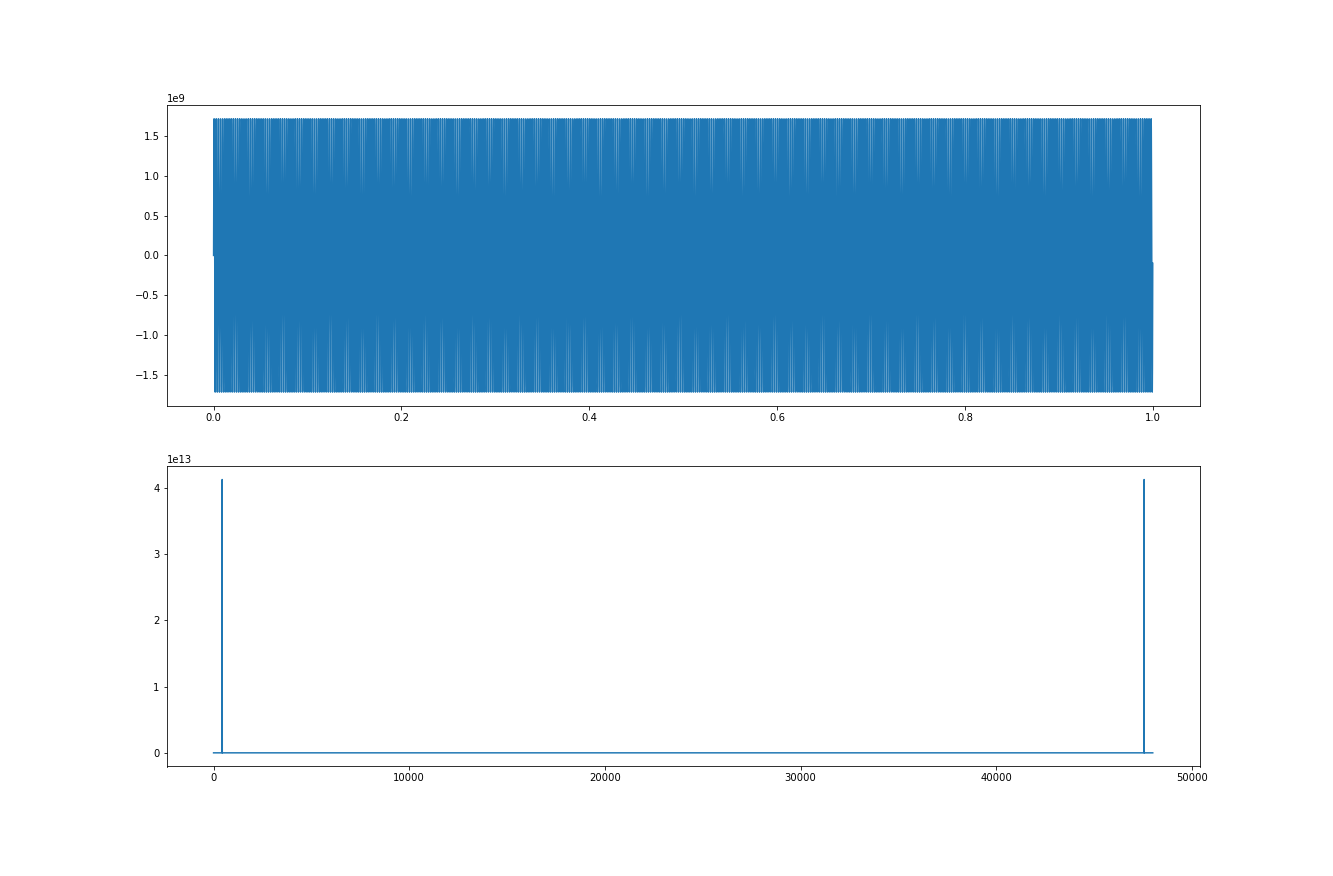
Kolejny przykład to moduł widma, ale w tym przypadku zmieniliśmy rozmiar transformaty Fouriera (w przykładzie do \(2^8=256\)), domyślny rozmiar jest zależny od długości sygnału. W przypadku Szybkiej Transformaty Fouriera, żeby odtworzyć w pełni sygnał, powinien być on pierwszą potęgą liczby \(2\), większą od długości naszego sygnału. W przypadku analizy naszego sygnału możemy go zmniejszyć, aby otrzymać mniej dokładane wyniki, ale w mniejszym nakładem czasu obliczeniowego oraz pamięci. Poniżej przykład, w którym zmniejszyliśmy rozmiar transformaty do 256. Oś OX w wykresie modułu widma została poprawiona, aby uwzględniać zmieniony jego rozmiar.
fsize=2**8Kroki pośrednie i przykłady modyfikacji widma.
plt.figure()
plt.subplot(2,1,1)
plt.plot(np.arange(0,data.shape[0])/fs,data)
plt.subplot(2,1,2)
yf = scipy.fftpack.fft(data,fsize)
plt.plot(np.arange(0,fs,fs/fsize),np.abs(yf))
plt.show()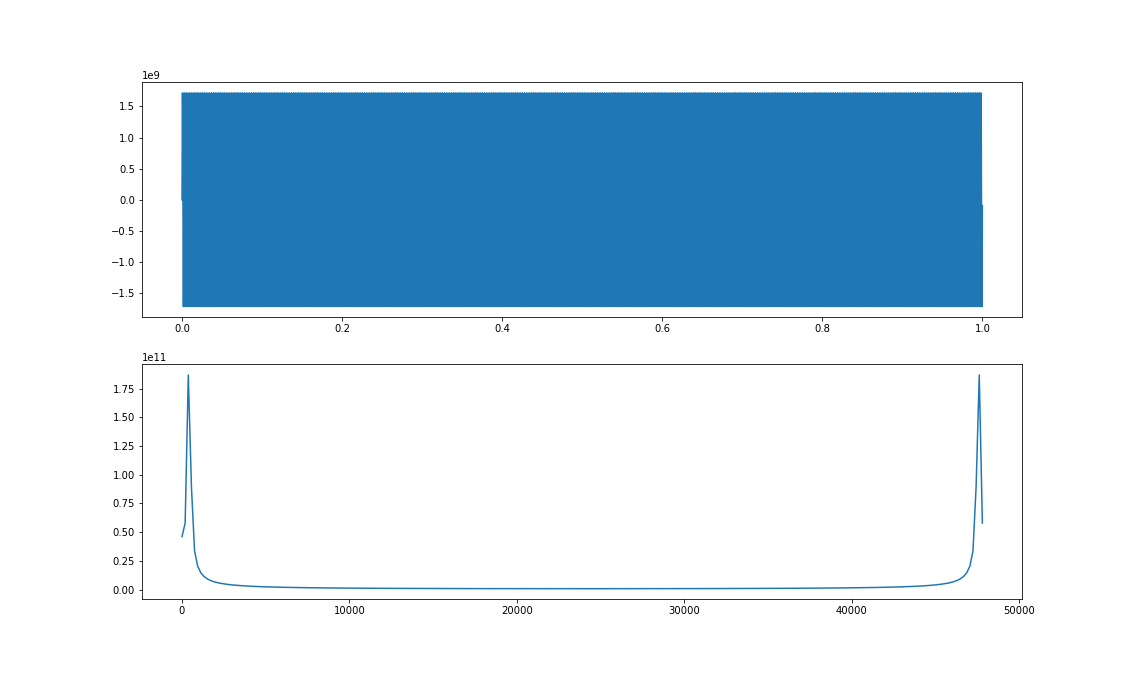
Kolejny etap wyświetlania modułu widma to wzięcie tylko połowy. Moduł widma jest symetryczny względem częstotliwości 0 Hz, więc przy jego wyświetlaniu możemy pominąć jedną z jego części:
plt.figure()
plt.subplot(2,1,1)
plt.plot(np.arange(0,data.shape[0])/fs,data)
plt.subplot(2,1,2)
yf = scipy.fftpack.fft(data,fsize)
plt.plot(np.arange(0,fs/2,fs/fsize),np.abs(yf[:fsize//2]))
plt.show()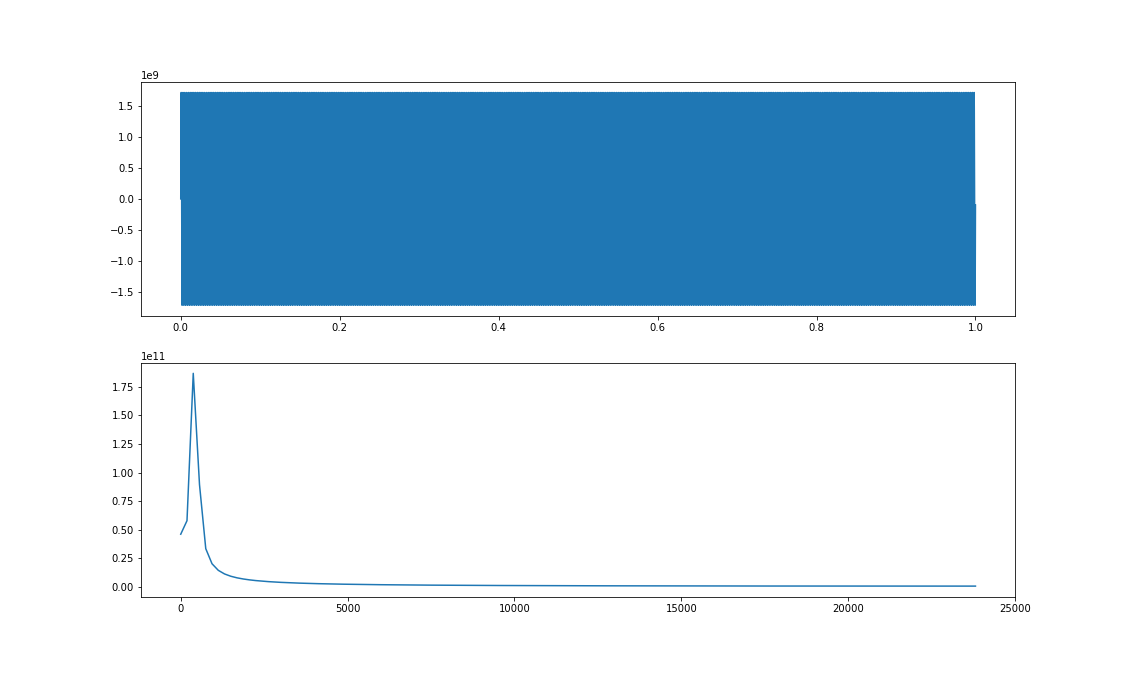
Ostatnią modyfikacją, którą możemy wykonać na naszym widmie, w celu ułatwienia jego wyświetlania jest przeskalowanie wartości widma do skali decybelowej (dB).
plt.figure()
plt.subplot(2,1,1)
plt.plot(np.arange(0,data.shape[0])/fs,data)
plt.subplot(2,1,2)
yf = scipy.fftpack.fft(data,fsize)
plt.plot(np.arange(0,fs/2,fs/fsize),20*np.log10( np.abs(yf[:fsize//2])))
plt.show()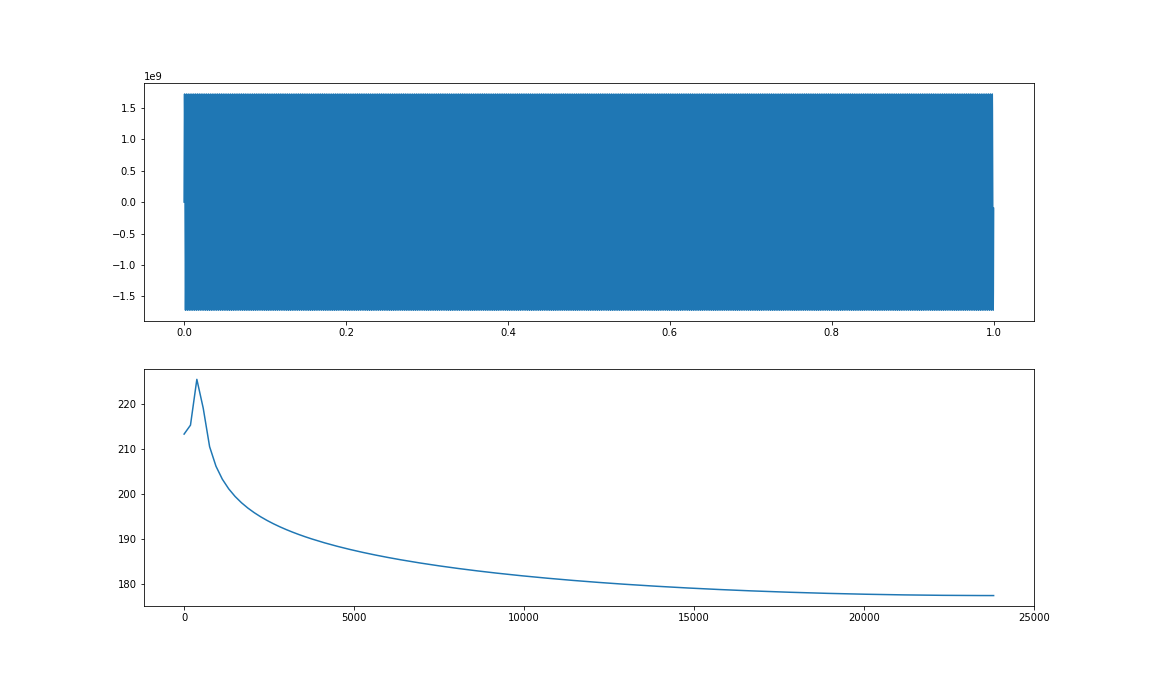
UWAGA! W powyższy sposób należy wyświetlać każde widmo, z jakim spotkacie się na zajęciach. Jedyny wyjątek będą stawiły niektóre szczególne przypadki, które będą dawały błędy dzielenia przez \(0\). W tych przypadkach warto wyświetlić widmo w skali liniowej i zastanowić się, czemu ten błąd wystąpił.
Zadanie Dźwięk 2
Celem zadania jest napisanie funkcji, którą będziecie wykorzystywać na przyszłych zajęciach do generowania wykresów. Funkcja ma przyjmować sygnał oraz częstotliwość próbkowania. Dodatkowy parametr pozwalający zawęzić fragment osi OX, żeby nie pokazywać całego sygnału, tylko jego fragment w celu zwiększenia czytelności (do tego wykorzystać plt.xlim()), domyślnie proszę ograniczyć to do jakiegoś zakresu. Funkcja powinna wyświetlić subplot składający się z dwóch wierszy. W górnym wierszu powinna wyświetlić się fragment sygnału dźwiękowego. W dolnym wierszu powinna zostać wyświetlona połówka widma w decybelach. Wszystkie osie powinny być odpowiednio oznaczone i wyskalowane, czyli górny wykres powinien na osi OX mieć sekundy, a dolny na osi OX powinien mieć częstotliwości, a osi OY decybele (dB). Proszę nie skalować osi OX dla widma. Wywołanie może wyglądać tak:
def plotAudio(Signal,Fs,TimeMargin=[0,0.02]):
#TODOWykonane zadanie zaprezentować na podstawie dołączonego pliku sin_440Hz.wav.
Automatyczne generowanie danych do pliku .docx jako podstawa sprawozdań
Poniżej znajdziecie fragment kodu pozwalający na automatyczne zapisywanie wykresów oraz wyników do dokumentu .docx. Pamiętajcie jednak, że tak wygenerowany dokument należy uzupełnić zwykle własną treścią, obserwacjami, podsumowaniem oraz wnioskami.
from docx import Document
from docx.shared import Inches
import matplotlib.pyplot as plt
import numpy as np
from io import BytesIO
document = Document()
document.add_heading('Zmień ten tytuł',0) # tworzenie nagłówków druga wartość to poziom nagłówka
files=['sin60Hz.wav','sin440Hz.wav','sin8000Hz.wav']
Margins=[[0,0.02],[0.133,0.155]]
for file in files:
document.add_heading('Plik - {}'.format(file),2)
for i,Margin in enumerate(Margins):
document.add_heading('Time margin {}'.format(Margin),3) # nagłówek sekcji, mozę być poziom wyżej
fig ,axs = plt.subplots(2,1,figsize=(10,7)) # tworzenie plota
############################################################
# Tu wykonujesz jakieś funkcje i rysujesz wykresy
############################################################
fig.suptitle('Time margin {}'.format(Margin)) # Tytuł wykresu
fig.tight_layout(pad=1.5) # poprawa czytelności
memfile = BytesIO() # tworzenie bufora
fig.savefig(memfile) # z zapis do bufora
document.add_picture(memfile, width=Inches(6)) # dodanie obrazu z bufora do pliku
memfile.close()
############################################################
# Tu dodajesz dane tekstowe - wartosci, wyjscie funkcji ect.
document.add_paragraph('wartość losowa = {}'.format(np.random.rand(1)))
############################################################
document.save('report.docx') # zapis do plikuZadanie Dźwięk 3
Wykorzystując kod generujący plik .docx oraz funkcję generującą wykresy z zadania 2, napisz skrypt analizujący pliki sin dołączone do instrukcji. W ramach programu trzeba będziemy sprawdzać 3 różne rozmiary parametru fsize=[2**8,2**12,2**16]. Dodatkowo będziemy sprawdzać, gdzie w naszym widmie (dla jakiej częstotliwości widma) dostaniemy jego najwyższą wartość. Dla każdego z tych generowanych wykresów wartość ta powinna znaleźć się automatycznie wygenerowana pod wykresem. Pomocna może być do tego funkcja np.argmax Można też zapisywać wartość amplitudy w tym miejscu. Do wykonania tego zadania potrzebne są 2 pętle (zamienić pętlę po marginesie czasu na pętlę z fsize) i niewielkie modyfikacje funkcji z zadania 2 (przekazanie zmiennej axs i zwrócenie danych). Na końcu sprawdzamy, czy poprawnie wygenerował nam się plik docx i zapisujemy go do formatu PDF.
Źródła danych dołączonych do instrukcji (nie pobierać)